Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 71

Um longo forno com formato hemicilíndrico (1 m de raio), usado para tratar termicamente folhas de produtos metálicos, tem três zonas. A zona de aquecimento (1) é construída com uma placa cerâmica de emissividade 0,85, que é operada a 1600 K por meio de queimadores de gás. Na zona de carga (2) estão as folhas metálicas, consideradas superfícies negras, que

devem ser mantidas a 500 K. A zona refratária (3) é fabricada com tijolos isolantes que têm uma emissividade de 0,6. Suponha condições de regime estacionário, superfícies cinzas e difusas, e que a convecção seja desprezível.

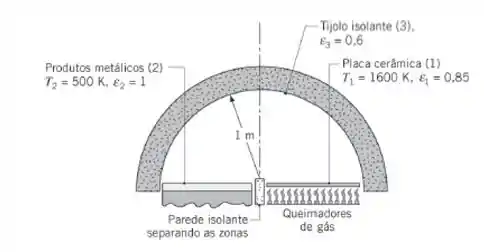
  1. Qual é a taxa de transferência de calor por unidade de comprimento do forno (normal à página) que deve ser suprida pelos queimadores de gás para as condições especificadas?

  2. Qual é a temperatura da superfície dos tijolos isolantes nas condições especificadas?

Passo 1

Vamos lá!! Temos um forno e queremos saber quanto de carlor vindo dos queimadores por unidade de comprimento é necessário para suprir as necessidades desse forno para os parâmetros dados no enunciado!

Em outras palavras, queremos q 1 ' , para isso vamos fazer um balanço de energia para a supefície 1 , lembrando que o forno é dividido em 3 zonas:

q 1 ' = A ' 1 F 12 J 1 - J 2 + A ' 1 F 13 J 1 - J 3

Mas se repararmos as disposições das zonas, vemos que a radiação que sai da superfície 1 não tem como chegar na superície 2 , logo:

q 1 ' = A ' 1 F 13 J 1 - J 3             ( 1 )

q 1 ' por sua vez pode ser escrito:

q 1 ' = E b 1 - J 1 1 - ε 1 ε 1 A ' 1                       ( 2 )

Agora, se fizermos o balanço de energia para a superfície 3 :

0 = A ' 3 F 31 J 3 - J 1 + A ' 3 F 32 ( J 3 - J 2 )

Lembrando que a superfície 2 é uma superfície negra, então J 2 = E b 2 !

Pela regra da simetria F 31 = F 32 , logo:

J 3 = J 1 + E b 2 2                       ( 3 )

Passo 2

Igualando ( 1 ) e ( 2 ) e substituindo 3 em ( 1 ) :

A ' 1 F 13 J 1 - J 1 + E b 2 2 = E b 1 - J 1 1 - ε 1 ε 1 A ' 1

Podemos cortar A ' 1 e pela regra da soma ( F 12 + F 13 = 1 ), F 13 = 1 , σ = 5,67 × 10 - 8 W / K 4 m 2 , substituindo:

J 1 - J 1 + 5,67 × 10 - 8 × 500 4 2 = 5,67 × 10 - 8 - J 1 1 - 0,85 0,85

Ficamos com:

J 1 = 341,748   W / m 2

Podemos achar J 3 :

J 3 = 341,748   + ( 5,67 × 10 - 8 × 500 4 ) 2 = 172,646   W / m 2

Passo 3

Podemos finalmente achar q 1 ' :

q 1 ' = A ' 1 F 13 J 1 - J 3    

Considerando que a parede isolante entre a superfície 1 e 2 tem espessura desprezível, então A 1 ' = 1 m :

q 1 ' = 1 × 1 341,748 - 172,646 = 169   W / m    

Passo 4

Agora queremos saber T 3 , lembrando que a superfície 3 éisolada, logo:

J 3 = E b 3 = σ T 3 4

Então:

T 3 = J 3 σ 1 4

Substituindo:

T 3 = 172,646 5,67 × 10 - 8 1 4

Calculando:

T 3 = 1320   K

Uhuuuul!!!

Resposta

q 1 ' = 169   W / m    

T 3 = 1320   K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um fluido criogênico escoa por um tubo com 20m m de diâmetro, cuja superfície externa é difusa e cinza, com uma emissividade de 0,0 5 e uma temperatura de 77K . Esse tubo é concêntrico a um tubo maior
Considere o sótão de uma casa localizada em um local de clima quente. O piso do sótão é caracterizado por uma largura L 1 = 8m , enquanto o telhado faz um ângulo de θ = 30 ° a partir da direção horizo
Um forno tem a forma de uma seção de cone truncado, como mostrado na figura. O piso do forno tem uma emissividade de ε 1 = 0,7 e é mantido a 1000K com um fluxo térmico de 2200W / m 2 . A parede latera
Considere as cavidades formadas por um cone, um cilindro e uma esfera que têm o mesmo tamanho de abertura ( d ) e dimensão principal ( L ) , como mostrado na figura.(a) Determine o fator de forma entr
Um forno cúbico, com 2m de lado, é usado para tratar termicamente uma placa de aço. A superfície superior do forno é formada por aquecedores elétricos radiantes que têm uma emissividade de 0,85 e são