Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 72

A base de um gerador de vapor de água com 200 mm de diâmetro é aquecido por radiação. O aquecedor, mantido a 1000°C e separado do gerador por uma dist��ncia de 100 mm, tem o mesmo diâmetro da base do destilador. As superfícies da base do gerador e do aquecedor são negras.

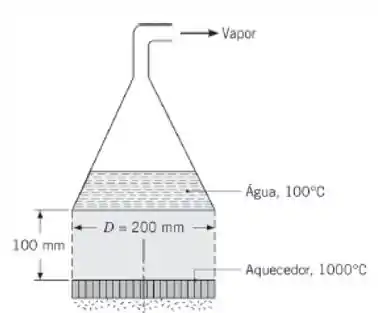
Por qual fator a taxa de produção de vapor poderia ser aumentada se os lados cilíndricos (superfícies tracejadas) estivessem isolados ao invés de estarem abertas para a vizinhança, mantida a 27°C?

Passo 1

Vamos lá!!! Temos um forno aquecendo a água e gerando vapor, e na letra a o problema quer saber a taxa de vapor aumentaria se os lados do forno fossem isolados!

A taxa de vapor é proporcional ao calor que chega até a água, q 2 , certo?!

Então a gente vai calcular a taxa de calor trocada duas vezes! A primeira com as laterais abertas e a segunda com as laterais isoladas pra ai sim calcular o aumento da taxa de vapor! Beleza?!

Então, vamos fazer um esqueminha simplificado da primeira situação, já com todos os dados no S I :

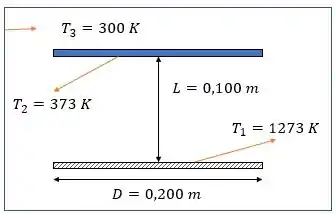
Podemos calcular q 2 i :

q 2 i = q 21 + q 23

Lembrando que as superfícies 1 e 2 são negras:

q 2 i = A 2 F 21 σ T 2 4 - T 1 4 + A 2 F 23 σ T 2 4 + T 3 4

Podemos isolar A 2 e σ :

q 2 i = A 2 σ F 21 T 2 4 - T 1 4 + F 23 T 2 4 + T 3 4

Passo 2

Precisamos de F 21 e F 23 !!

O que temos são discos paralelos coaxiais, para descobrir F 21 , vamos usar as relações da tabela 13.2 :

R 1 = R 2 = r L = 100 2 100 = 1

S = 1 + 1 + R 2 2 R 1 2 = 1 + 1 + 1 2 1 2 = 3

Para calculr F 12 :

F 21 = 1 2 S - S 2 - 4 D 2 D 1 2 1 2

Substituindo:

F 21 = 1 2 3 - 3 2 - 4 100 100 2 1 2 = 0 , 38

Pela regra da soma:

F 21 + F 23 = 1

Logo:

F 23 = 1 - 0,38 = 0,62

Se σ = 5,67 × 10 - 8 W / m 2 K 4 :

q 2 i = π × 0,200 2 4 × 5,67 × 10 - 8 × 0,38 × 373 4 - 1273 4 + 0,62 300 4 - 1273 4  

Calculando:

q 2 i = - 1752   W

Passo 3

Agora vamos para a segunda situação, a gente vai colocar paredes isolantes no forno:

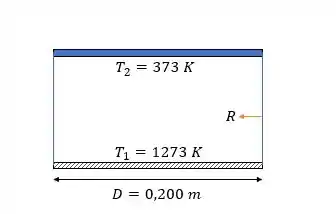
Queremos achar q 2 f e temos uma superfície isolada, então vamos usar a equação 13.27 :

q 2 f = A 2 σ ( T 2 4 - T 1 4 ) 1 - ε 1 A 1 ε 1 + 1 A 1 F 12 + 1 A 1 F 1 R + 1 A 2 F 2 R - 1 + 1 - ε 2 A 2 ε 2

Como A 1 = A 2 e as superfícies 1 e 2 são negras com ε 1 = ε 2 = 1 , ficamos com:

q 2 f = A 2 σ ( T 2 4 - T 1 4 ) 1 F 12 + 1 F 1 R + 1 F 2 R - 1

Pela regra da soma:

F 1 R = 1 - F 12 = 1 - 0,38 = 0,62

Pela regra da simetria:

F 1 R = F 2 R

Substituindo:

q 2 f = π × 0,2 2 4 × 5,67 × 10 - 8 ( 327 4 - 1273 4 ) 1 0,38 + 1 0,62 + 1 0,62 - 1

Calculando:

q 2 f = - 3204   W

Passo 4

Como discutimos no passo 1 o aumento da taxa de produção de vapor é proporcional ao aumento da taxa de transferência de calor, logo:

q 2 f q 2 i = - 3204 - 1752 = 1,83

A taxa de vapor vai aumentar em um fator de 1,83 !

Uhuuuu!!!!

Resposta

A taxa de vapor vai aumentar em um fator de 1,83 !

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois discos planos coaxiais estão separados por uma distância L = 0 , 8 0m . O disco inferior ( A 1 ) é sólido e tem um diâmetro D e = 0,80m e uma temperatura T 1 = 300K . O disco superior ( A 2 ) , a
Um orifício com fundo plano e 8m m de diâmetro é perfurado até uma profundidade de 24m m em um material cinza e difuso, que tem uma emissividade de 0,8 e uma temperatura uniforme de 1000K .(a) Determi
Considere uma janela de vidro duplo. A superfície do vidro pode ser tratada com um revestimento de baixa emissividade para reduzir sua emissividade de ε = 0,95 para ε = 0,05 . Determine o fluxo térmic
A configuração mostrada é usada para calibrar um medidor de fluxo térmico. O medidor tem uma superfície negra com 8m m de diâmetro, que é mantida a 1 7 ° C por uma placa de suporte resfriada com água.
Considere discos negros, paralelos e coaxiais, separados por uma distância de 0,20m . O disco inferior, com diâmetro de 0 , 2 0m , é mantido a 500K , enquanto a vizinhança está a 3 1 0K .Qual será a t