Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 111
Analise o escoamento através de uma expansão súbita, aplicando as equações básicas a um volume de controle começando na expansão e terminando a jusante dela (admita que a pressão de entrada age sobre a área na expansão). Desenvolva uma expansão e trace um gráfico da perda de carga menor através da expansão como uma função da razão de áreas, e compare os dados da Fig. 8.15.
Passo 1
Equações:
- Massa:
- Momento:
- Energia:
Considerações:
- Escoamento Estacionário;
- Fluido Incompressível;
- Escoamento Uniforme;
- Sem Ação de Forças de Corpo;
- Sem Trabalho;
- Sem Forças de Resistência;
- Ação da Gravidade Desprezada.
Passo 2
Realizando as considerações do Passo 1.
Para a Equação de Massa:
Para a Equação de Momento:
Aplicando a Equação de Massa.
Para a Equação de Energia:
Aplicando a Equação de Massa e sabendo que .
Combinando as equações obtidas da Equação do Momento e de Energia, temos:
Rearranjando:
Passo 3
Temos que:
Substituindo na equação obtida no Passo 2:
Temos que:
Passo 4
Com a equação obtida, podemos traçar o gráfico da perda de carga menor através da expansão como uma função da razão de áreas e comparando os dados da Fig. 8.15.
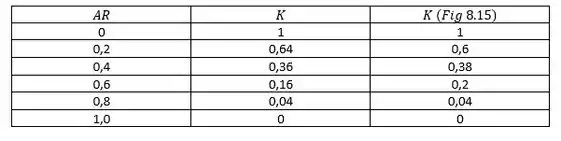
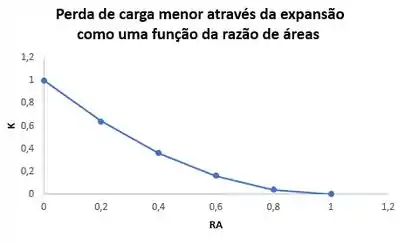
Resposta
Discursiva