Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 91
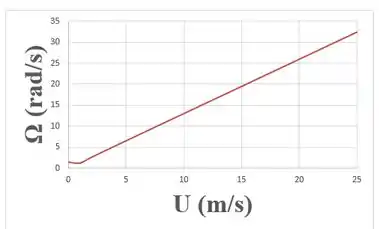
Um anemômetro de conchas usa duas semiesferas ocas de 5 cm de diâmetro conectadas a barras de 15 cm, como na Figura P7.91. O arrasto nas barras é desprezível, e o rolamento central tem um torque resistente de 0,004 N.m. Levantando hipóteses simplificadoras para uma média da geometria variável com o tempo, calcule e plote a variação da taxa de rotação do anemômetro Ω com a velocidade do vento U na faixa de 0
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
Nessa questão, temos um anemômetro formado por duas barras de comprimento cada e duas semiesferas de diâmetro , e umângulo de rotação como mostra a figura que ilustra a questão.
Segundo o enunciado, o arrasto nas barras é desprezível e o sistema tem um torque de . O vento tem velocidade variando na faixa .
O enunciado então nos pede pra plotar um gráfico de , na faixa dada pelo enunciado, e . Pra isso, teremos que deduzir uma expressão matemática para o balanço de momento entre as duas semiesferas do anemômetro.
Mas antes da gente ir pro Passo 2, vamos lembrar que para o ar à temperatura ambiente, a massa específica será e a viscosidade será .
Então vem comigo pra gente resolver esse problema juntos!
Passo 2
Nosso primeiro passo será encontrar uma expressão para o torque .
Pra isso, vamos considerar o esquema abaixo:
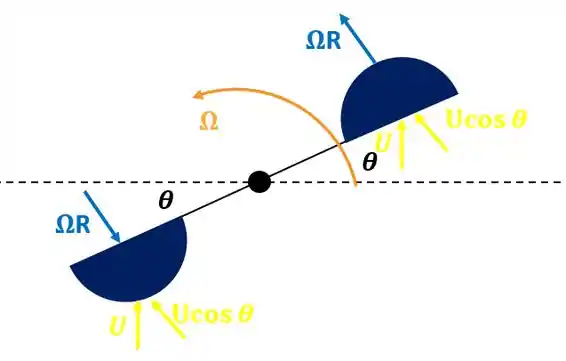
Como vocês podem ver, temos um ângulo de varredura entre a barra e o eixo horizontal. Dessa maneira, componente da velocidade da velocidade agindo nas duas semiesferas.
Além disso, também temos a velocidade devido à rotação da barra agindo nas semiesferas que é leva em conta a velocidade angular e o raio da esfera, ou seja .
Sendo assim, podemos fazer um balanço de momento, considerando a linha de ação da força de arrasto das semiesferas:
Os coeficientes de arrasto podem ser encontrados na Tabela 7.3, Página 495. , como na imagem:
Ou seja, e .
Além disso, devemos calcular as velocidades relativas e . Pra isso, devemos fazer um balanço entre as velocidades e , levando em consideração os sentidos delas.
Na primeira delas, as velocidades estão no mesmo sentido, e, portanto, . Na segunda, as velocidades têm sentido diferente, e, portanto,.
Substituindo no nosso balanço:
Passo 3
Por fim, pra resolver a questão, devemos plotar um gráfico de , na faixa dada pelo enunciado, e .
Pra fazer uma simplificação, devemos considerar que o torque médio de se repete cada ângulo de . Dessa maneira, definimos que a média de variando de a , é .
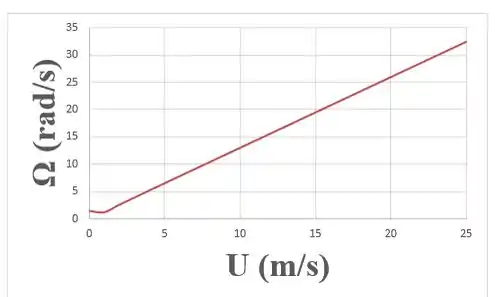
Pronto, matamos a questão juntos!
Resposta
O gráfico plotado foi
