Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 25

Uma aplicação importante da mecânica dos fluidos é o estudo da ventilação de uma sala. Em particular, suponhamos que há uma fonte 5 (massa por unidade de tempo) de poluição do ar em uma sala de volume V (Figura P7-25). Os exemplos incluem o monóxido de carbono da fumaça do cigarro ou um aquecedor à querosene sem ventilação, os gases como a amónia dos produtos de limpeza de uma casa e os vapores liberados pela evaporação dos compostos orgânicos voláteis (VOCs) de um contêiner aberto. Seja c a concentração de massa (a massa do contaminante por unidade de volume de ar). V ˙ é a vazão em volume de ar fresco que entra na sala. Se o ar da sala estiver bem misturado para que a concentração de massa c seja uniforme em toda a sala, mas varie com o tempo, a equação diferencial da concentração de massa na sala como função do tempo é

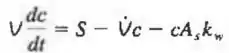
onde k w é um coeficiente de adsorção e A s é a área da superfície das paredes, pisos, móveis etc. que absorvem parte do contaminante. Escreva as dimensões primárias dos três primeiros termos aditivos da equação, e certifique-se de que esses termos são dimensionalmente homogêneos. Em seguida, determine as dimensões de k w . Mostre todo o seu trabalho.

Passo 1

Oi pessoal, tudo bem?

Primeiramente vamos relembrar as dimensões primárias de cada termo citado pelo problema:

1. As dimensões primárias da derivada do tempo ( d / d t ) são 1 / t e m p o .

2. Os de A s são c o m p r i m e n t o ² ,

3. Os de V são c o m p r i m e n t o ³ ,

4. Os de c são m a s s a / c o m p r i m e n t o ³ e

5. Os de V são c o m p r i m e n t o ³ / t e m p o .

6. S é m a s s a / t e m p o (como o problema informa)

Vamos agora ver se a equação é dimensionalmente homogênea.

Passo 2

Para relembrar a equação diferencial da concentração de massa na sala como função do tempo:

V d c d t = S - V ˙ c - c A s k w

Assim, cada termo na equação pode ser escrito em termos de dimensões primárias:

Primeiramente:

V d c d t = c o m p r i m e n t o 3 ⋅ m a s s a c o m p r i m e n t o 3 ⋅ 1 t e m p o = m a s s a t e m p o   ;

S = m a s s a t e m p o   ;

V ˙ c = c o m p r i m e n t o 3 t e m p o ⋅ m a s s a c o m p r i m e n t o 3 = m a s s a t e m p o

Passo 3

De fato, os três primeiros termos aditivos têm as mesmas dimensões { m 1 t - 1 }. Como a equação deve ser dimensionalmente homogênea, o último termo também deve ter as mesmas dimensões.

Então, usamos esse fato para encontrar as dimensões de k w :

c A s k w = m a s s a c o m p r i m e n t o 3 ⋅ c o m p r i m e n t o 2 ⋅ k w = m a s s a t e m p o

Reorganizando os termos:

k w = m a s s a t e m p o ⋅ 1 c o m p r i m e n t o 2 ⋅ c o m p r i m e n t o 3 m a s s a = c o m p r i m e n t o t e m p o

Resposta

Portanto, foi provado que a equação é dimensionalmente homogênea e:

k w = c o m p r i m e n t o t e m p o

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em uma tabela periódica dos elementos, a massa molar M , também chamada p e s oa t ô m i c o ô , quase sempre é listada como se fosse uma quantidade adimensional (Figura P7-5). Na verdade, o p e s oa
Escreva as dimensões primárias de cada uma das seguintes variáveis do estudo da transferência de calor por convecção (Figura P7-16), mostrando todo o seu trabalho: a taxa de geração de calor g ˙ . (Di
A condutividade térmica k é uma medida da capacidade de um material de conduzir calor (Figura P7-15). Para a transferência de calor na direção x , através de uma superfície normal à direção x , a lei
Definimos a c o n s t a n t ee s p e c í f i c ad og á si d e a lR g á s í á á para um determinado gás como a relação entre a constante universal dos gases e a massa molar (também chamada p e s om o l
Considere a situação comum na qual um pesquisador está tentando comparar o número de Reynolds de um grande veículo protótipo com aquele de um modelo em pequena escala em um túnel de vento. É melhor qu