Um chip quadrado, com lado , opera em condições isotérmicas. O chip é posicionado em um substrato de modo que suas superfícies laterais e inferior estão isoladas termicamente, enquanto sua superfície superior encontra-se exposta ao escoamento de um refrigerante a . A partir de considerações de confiabilidade, a temperatura do chip não pode exceder a .

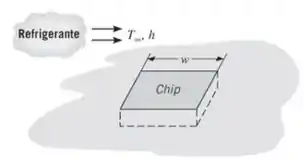
Sendo a substância refrigerante o ar, com um coeficiente de transferência de calor por convecção correspondente qual é a potência máxima permitida para o chip? Sendo o refrigerante um líquido dielétrico para o qual qual é a potência máxima permitida?

Aqui vamos assumir que:

1. Estamos em condição de estado estacionário;
2. A transferência de calor é desprezível nos lados e no fundo do chip;
3. O chip está a uma temperatura uniforme (isotérmica);
4.  A transferência de calor por radiação no ar é desprezível.

Belezinha, com isso em mente vamos ter que toda a energia elétrica dissipada no chip é transferida por convecção ao fluido refrigerante. Então,

E pela Lei de Newton de resfriamento, temos:

Como o chip é quadrado, sua área é definida por:

Então,

Agora podemos calcular a potência máxima para as duas situações.

Se o nosso fluido refrigerante for o ar vamos ter que:

Para o líquido dielétrico temos,

Com isso vemos que o ar é um fluido de baixa transferência de calor. Portanto, no ar, o chip pode dissipar muito menos energia do que no líquido dielétrico.