Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 125
Um aquecedor radiante, que é usado em processos de tratamento de superfícies, é constituído por um longo elemento aquecedor com formato cilíndrico e diâmetro D1 = 0,005 m, com emissividade ε1 = 0,80. O aquecedor é parcialmente envolvido por um refletor parabólico longo e delgado, cujas emissividades das superfícies interna e externa são ε2i = 0,10 e ε2e = 0,80, respectivamente. As áreas superficiais interna e externa, por unidade de comprimento do refletor, são cada uma de , enquanto o coeficiente convectivo médio nas superfícies interna e externa é de . O sistema pode ser considerado no
interior de um meio quiescente e infinito composto por ar atmosférico a , estando exposto a uma grande vizinhança a Tviz = 300 K.
- Esboce o circuito de radiação apropriado e escreva expressões para cada uma das resistências da rede.
- Se, sob condições de regime estacionário, potência elétrica é dissipada no aquecedor a e a temperatura superficial do aquecedor é T1 = 1200 K, qual é a taxa líquida na qual a energia radiante é transferida do aquecedor?
- Qual é a taxa líquida na qual energia radiante é transferida do aquecedor para a vizinhança?
- Qual é a temperatura,T2, do refletor?
Passo 1
Falaaaaaa galerinha !!
Vamos seguindo?
Bom, a letra (a) nos pediu apenas para esquematizar todo o circuito elétrico, certo?
Então, dispondo todos os acontecimentos descritos no problema nós vamos obter:
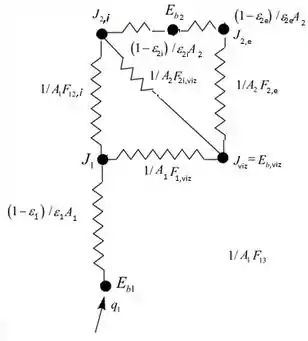
Agora, a letra (b) nos pediu para a taxa líquida na qual a energia radiante é transferida do aquecedor
Para isso nós podemos começar fazendo o balanço de energia, sabendo que a potência fornecida é transferida por convecção e radiação:
Vamos procurar achar primeiro o calor convectivo:
Sabemos que:
O coeficiente convectivo nós podemos calcular:
Lembrando que:
Para achar as propriedades do ar nós precisamos da temperatura média:
Assumindo que a temperatura seja próxima a e olhando na Tabela A – 4:
Substituindo:
E para o coeficiente:
No calor:
E agora ficou topzeraa !!
Vamos substituir:
E assim finalizamos a letra (b) !!
Passo 2
A letra (c) nos pede para achar a taxa líquida na qual energia radiante é transferida do aquecedor para a vizinhança, ok?
A transferência radiante é dada pela fórmula:
Vamos ver o que podemos calcular:
Só não temos né?!
Para acha-lo nós vamos usar uma relação similar à anterior, mas para a radiação que entra na superfície 1:
Para este nós temos todos os valores e só vamos substituir:
Na equação entre a superfície 1 e a vizinhança:
Passo 3
Shoow !! Para finalizar nós vamos fazer a letra (d) !! Nela nós queremos achar a temperatura,, do refletor, Tranquilinha?
Para acha-la nós precisamos achar a potência emissiva da superfície 2 que se relaciona com a temperatura assim:
Vamos começar fazendo o balanço para a superfície 2:
Vamos ver a fórmula para cada uma delas?
Nós já temos:
Só precisamos então da radiosidade
Usando para isso a radiosidade no refletor:
Lembrando que:
Então:
Agora é só substituir:
Agora siiim!!
Resolvendo:
Cansou, não foi !? Mas acabamos !!