Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 10

A relação de reciprocidade, a regra da soma e as Equações 13.5 a 13.7 podem ser usadas para desenvolver relações para o fator de forma que permitem a utilização das Figuras 13.4 e/ou 13.6 para configurações mais complexas. Considere o fator de forma F 14 para as superfícies 1 e 4 na geometria a seguir. Essas superfícies são perpendiculares, porém não têm uma aresta comum.

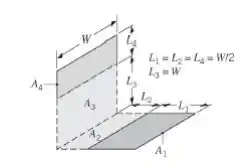
Obtenha a seguinte expressão para o fator de forma F 14 :

F 14 = 1 A 1 A 1 + A 2 F 1,2 3,4 + A 2 F 23 - A 1 + A 2 F 1,2 3 - A 2 F 2 3,4

Se L 1 = L 2 = L 4 = W 2 e L 3 = W , qual é o valor de F 14 ?

Passo 1

Nessa questão nós temos a disposição de superfícies perpendiculares sem aresta comum. E queremos encontrar uma relação para o fator de forma F 14 e o valor de F 14 para as dimensões prescritas.

Passo 2

Para resolver essa questão vamos assumir superfícies difusas. Para determinar F 14 , é conveniente definir as superfícies hipotéticas A 2 e A 3 . Da Eq. 13,6,

A 1 + A 2 F ( 1,2 ) ( 3,4 ) = A 1 F 1 ( 3,4 ) + A 2 F 2 ( 3,4 )

Onde F 1,2 3,4 e F 2   3,4 podem ser obtidos na Fig. 13.6. Substituindo A 1 F 1 ( 3,4 ) e combinando as expressões, encontramos:

A 1 F 1 ( 3,4 ) = A 1 F 13 + A 1 F 14

F 14 = 1 A 1 A 1 + A 2 F 1,2 3,4 - A 1 F 13 - A 2 F 2 ( 3,4 )

Substituindo A 1 F 13 , que pode ser expresso como:

A 1 + A 2 F 1,2 3 = A 1 F 13 + A 2 F 23

A relação desejada é então,

F 14 = 1 A 1 A 1 + A 2 F 1,2 3,4 + A 2 F 23 - A 1 + A 2 F 1,2 3 - A 2 F 2 3,4

Passo 3

Para as dimensões dadas e usando a Fig. 13.6, encontramos:

Superfícies 1,2 3,4 :

Y X = L 1 + L 2 W = 1

Z X = L 3 + L 4 W = 1,45

F ( 1,2 ) ( 3,4 ) = 0,22

Superfícies 23 :

Y X = L 2 W = 0,5

Z X = L 3 W = 1

F 23 = 0,28

Superfícies 1,2 3 :

Y X = L 1 + L 2 W = 1

Z X = L 3 W = 1

F ( 1,2 ) 3 = 0,20

Superfícies   2 3,4 :

Y X = L 2 W = 0,5

Z X = L 3 + L 4 W = 1,5

F 2 ( 3,4 ) = 0,31

Usando a relação do passo anterior, encontramos:

F 14 = 1 W L 1 W L 1 + W L 2 0,22 + W L 2 0,28 - W L 1 + W L 2 0,20 - W L 2 0,31

F 14 = 2 0,22 + 1 0,28 - 2 0,20 - 1 0,31 = 0,01

Resposta

F 14 = 0,01

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um forno de laboratório tem uma câmara interna cúbica com 1 m de lado, com superfícies interiores com emissividade ε = 0,85. Determine a taxa de transferência de calor radiante inicial para o laborató
Uma cabine de observação está localizada diretamente acima da linha de um laminador a quente, como mostrado na figura. O piso da cabine está exposto a uma porção da lâmina quente, que está a uma tempe
Um pequeno forno é constituído por uma caixa cúbica, de lado L = 0,1 m, como mostrado. O piso da caixa é constituído por um aquecedor que fornece P = 400 W. As paredes restantes perdem calor para a vi
Uma placa cinza, difusa e opaca ( 200m mx200m m ) , com uma emissividade de 0,8, é colocada sobre a abertura de um forno e sabe-se que, em um determinado instante, ela se encontra a 400 K. A base do f
Uma ferramenta para o processamento de pastilhas de silício está posicionada no interior de uma câmara de vácuo cujas paredes são negras e mantidas a T c v=300K , por um refrigerante. A fina pastilha