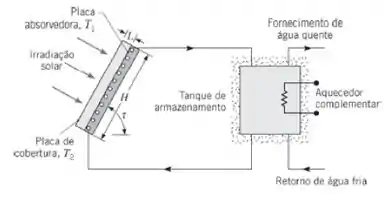
Considere o coletor solar plano apresentado no Problema 9.98. A placa de absorção tem um revestimento para o qual ε1 = 0,96 e a placa de cobertura tem uma emissividade de ε2 = 0,92. Com relação à troca radiante, as duas placas podem ser aproximadas por superfícies cinzas e difusas.

1. Para as condições do Problema 9.98, qual é a taxa de transferência de calor por convecção natural que sai da placa de absorção e a taxa radiante líquida entre as placas?
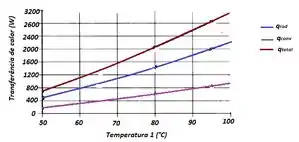
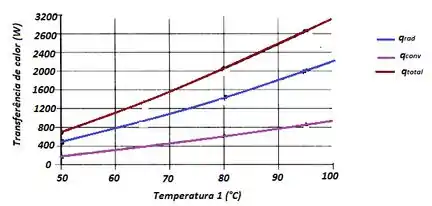
2. A temperatura da placa absorvedora varia de acordo com a vazão do fluido de trabalho que escoa através dos tubos em sua face inferior. Com todos os demais parâmetros permanecendo como especificados, calcule e represente graficamente as taxas de transferência de calor por convecção natural e por radiação como funções da temperatura da placa de absorção, para 50 ≤ T1 ≤ 100°C.

É isso ai galerinhaaa !! Vamos continuando?

Nós temos duas perguntas a serem respondidas na letra (a), primeiro precisamos achar a convecção, tudo bem?

Para o calor convectivo:

Do problema 9.98 nós temos:

Só nos falta o coeficiente convectivo, mas ele pode ser calculado como:

Sabendo que:

Na fórmula:

Nós já sabemos que:

Para achar as propriedades do ar nós precisamos da temperatura média:

Assumindo que a temperatura seja próxima a e olhando na Tabela A – 4:

Substituindo:

Colocando no calor:

Shooow, encontramos a primeira resposta !! Bora pra segunda?