Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 23
Um aquecedor tubular com a superfície interna negra de temperatura uniforme irradia um disco que se encontra em posição coaxial ao tubo.
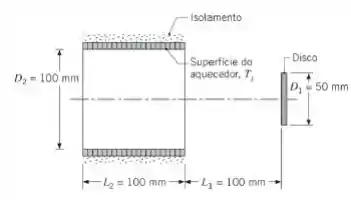
(a) Determine a potência radiante oriunda do aquecedor que incide sobre o disco, . Qual é a irradiação sobre o disco, ?
(b) Para diâmetros do disco de , e , represente graficamente e como funções da distância de separação para .
Passo 1
Nessa questão nós temos um qquecedor tubular que irradia como corpo negro a . A partir disso vamos encontrar a potência radiante da superfície do aquecedor, , interceptada por um disco, , em um local prescrito e a irradiação no disco,
Passo 2
Para resolver essa questão vamos assumir que a superfície do aquecedor se comporta como corpo negro com temperatura uniforme e que as superfícies têm radiosidade e irradiação uniformes.
A potência radiante que sai da superfície interna do aquecedor tubular que é interceptada pelo disco é:
Onde o aquecedor é a superfície 2 e o disco é a superfície 1. Segue da regra de reciprocidade que,
Passo 3
Definindo agora os discos hipotéticos e , localizados nas extremidades do aquecedor tubular. Por inspeção, segue-se que:
Ou,
Onde e podem ser determinados a partir da Fig. 13.5. Substituindo os valores numéricos, com :
Com,
E,
Com,
Passo 4
Então, temos que a potência radiante que sai da superfície interna do aquecedor tubular que é interceptada pelo disco é:
Substituindo os valores,
Onde,
A irradiação originária da emissão que sai da superfície do aquecedor é,
Resposta
- e