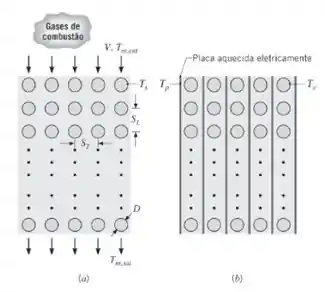
Um gerador de vapor é constituído por um feixe alinhado de tubos, cada um com diâmetro externo D = 10 mm e comprimento L = 1 m. Os passos longitudinal e transversal são SL = ST = 20 mm, enquanto os números de colunas nas direções longitudinal e transversal são NL = 20 e NT = 5. Água saturada (no estado líquido) entra nos tubos a uma pressão de 2,5 bar e sua

vazão é ajustada de modo a assegurar que ela deixa os tubos como vapor saturado. A ebulição que ocorre nos tubos mantém uma temperatura na parede dos tubos uniforme de 400 K.

1. Considere o caso (a) no qual produtos de combustão entram no feixe de tubos com uma velocidade e temperatura de V = 10 m/s e Tm,ent = 1200 K, respectivamente. Determine o coeficiente convectivo médio no lado do gás, a temperatura de saída do gás e a taxa de produção de vapor em kg/s. As propriedades do gás podem ser aproximadas por aquelas do ar atmosférico a uma temperatura média de 900 K.
2. Um projeto alternativo de gerador de vapor, caso (b), é constituído pelo mesmo arranjo de tubos, porém o escoamento do gás é substituído por um espaço onde há vácuo com placas eletricamente aquecidas introduzidas entre cada coluna de tubos. Se as placas são mantidas a uma temperatura uniforme de Tp = 1200 K, qual é a taxa de produção de vapor? As superfícies das placas e dos tubos podem ser aproximadas por corpos negros.
3. Considere condições nas quais as placas estão instaladas, como no caso (b), e produtos de combustão a temperaturas elevadas escoam sobre os tubos, como no caso (a). As placas não são mais aquecidas eletricamente, mas sua condutividade térmica é suficientemente elevada para assegurar uma temperatura uniforme nas placas. Comente a respeito dos fatores que influenciam a temperatura da placa e a distribuição de temperaturas no gás. Estabeleça um contraste (qualitativo) entre a temperatura de saída do gás e a taxa de geração de vapor em relação aos resultados do caso (a).

É isso ai galerinhaaa !! Vamos continuando?

Bom, antes de qualquer coisa, a letra (a) nos pediu três coisas: o coeficiente convectivo médio no lado do gás, a temperatura de saída do gás e a taxa de produção de vapor em kg/s, ok?

Bom galerinha, a primeira coisa que vamos achar é o coeficiente convectivo, mas antes de calcular nós precisamos achar o Reynolds, não é?

Para o ar a 900 K podemos achar as propriedades na Tabela A – 4:

Só precisamos achar a velocidade máxima, mas ela é dada por uma fórmula:

O problema nos deu tudo que precisávamos:

Então é só substituir:

Calculando o Reynolds:

Neste caso nós podemos usar a seguinte fórmula para calcular o coeficiente:

Só não temos o Prandtl para o ar a 400 K, mas na Tabela A – 4:

Substituindo:

Agora precisamos da temperatura de saída do gás !! E para isso nós também temos uma fórmula bem conhecida de vocês:

Podemos reescrever esta equação como:

Sabemos que:

Shooow de bolinhasss !! Vamos substituir:

E a última pergunta é, qual a taxa de produção de vapor em kg/s?

A vazão mássica pode ser calculada como:

O calor é perdido por convecção nós podemos reescrevê-lo como:

Substituindo

Agora que temos tudo é só substituir, lembrando que tabelado nós temos:

Então: