Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 124
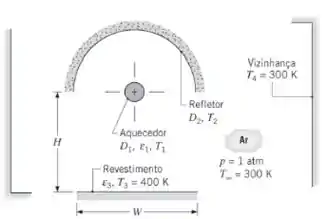
Um longo aquecedor na forma de bastão, com diâmetro D1 = 10 mm e emissividade ε1 = 1,0, encontra-se posicionado coaxialmente a um refletor semicilíndrico isolado termicamente com diâmetro D2 = 1 m. Um longo painel, com largura W = 1 m, está alinhado com o refletor e está separado do aquecedor por uma distância H = 1 m. O painel está revestido com uma tinta especial (ε3 = 0,7), que é curada pela sua manutenção a 400 K. O painel é isolado termicamente no seu lado posterior e todo o sistema está localizado no interior de uma grande sala onde as paredes e o ar atmosférico quiescente estão a 300 K. A transferência de calor por convecção pode ser desprezada na superfície do refletor.
- Esboce o circuito térmico equivalente ao sistema e identifique todas as resistências e potenciais pertinentes.
- Expressando os seus resultados em termos das variáveis apropriadas, escreva o sistema de equações necessário para determinar as temperaturas do aquecedor e do refletor, T1 e T2, respectivamente. Determine essas temperaturas para as condições especificadas.
- Determine a taxa na qual deve ser suprida potência elétrica, por unidade de comprimento, ao bastão aquecedor.
Passo 1
Falaaaaaa galerinha !!
Vamos seguindo?
Bom, a letra (a) nos pediu apenas para esquematizar todo o circuito elétrico, certo?
Então, dispondo todos os acontecimentos descritos no problema nós vamos obter:
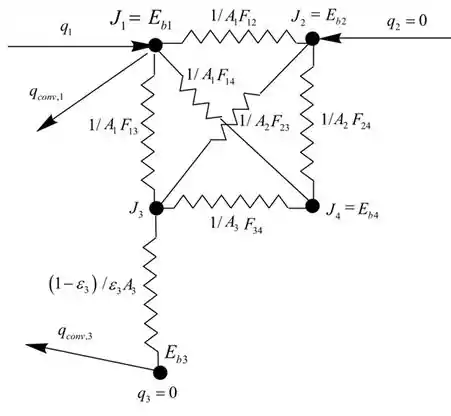
Agora, a letra (b) nos pediu para achar
Para isso nós podemos começar fazendo o balanço de energia para as superfícies 1, 2 e 3 olhando a figura acima:
Tá difícil, não é? Mas podemos começar pelo balanço da superfície 3!!
Lembrando do calor convectivo e da potência emissiva:
Vamos ver o que temos:
O coeficiente convectivo nós podemos calcular:
Lembrando que:
Neste caso:
Para achar as propriedades do ar nós precisamos da temperatura média:
Assumindo que a temperatura seja próxima a e olhando na Tabela A – 4:
Substituindo:
E para o coeficiente:
Agora sim !! Vamos colocar na fórmula:
Também podemos achar a potência emissiva para a superfície 4:
Substituindo:
Passo 2
Agora nós queremos achar os fatores de forma!!
Pela simetria nós podemos concluir que:
Aplicando o somatório e a reciprocidade nós achamos mais algumas:
Para achar os demais nós vamos precisar chamar a superfície traçada sobre o diâmetro da superfície 2, passando sobre a superfície 1, que vamos chamar agora de 2’.
Neste caso, a superfície 3 e 2’ foram superfícies paralelas, olhando na figura:
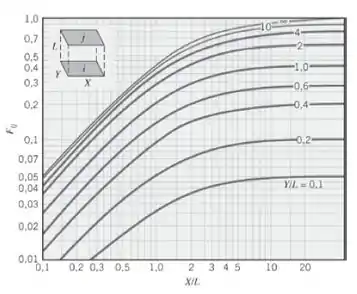
Para:
Então:
Lembrando que:
Então:
Para a superfície 2 e 2’:
Usando a reciprocidade:
Então:
E o somatório para a superfície 2:
Já vimos que:
E o somatório:
Ufaaa !!
Passo 3
Foi pesado, não é? Mas agora podemos colocar tudo isso na fórmula do balanço da superfície 3:
Agora, se usarmos no balanço da superfície 2:
Resolvendo as duas equações:
E usando a fórmula das potências emissivas:
Substituindo:
Passo 4
Maaasss, nós não acabamos !!
Queremos, na letra (c), determine a taxa na qual deve ser suprida de potência elétrica, por unidade de comprimento, ao bastão aquecedor!
Neste caso nós precisamos achar lá no balanço do passo 1:
Reorganizando pra gerar o que queremos, :
Só que também não é o que queremos:
Substituindo:
Nós ainda temos o calor convectivo, mas nós podemos achar:
Para o coeficiente é convectivo precisamos começar achando
Para achar as propriedades do ar nós precisamos da temperatura média:
Assumindo que a temperatura seja próxima a e olhando na Tabela A – 4:
Substituindo:
E para o coeficiente:
Substituindo:
Então já conseguimos calcular a convecção:
Colocando na fórmula para achar o que queremos:
Ufaaaa!! Deu um trabalhão, mas conseguimos !!