Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 10.Problemas - Ex. 22
Um aqueduto trapezoidal (figura 10.7) tem b = 5 m e e tem uma vazão normal de 60 m³/s de água quando . Para superfícies em tijolo de barro, calcule a queda de elevação necessária em m/km.
Passo 1
Fala aí, galera!!! Bora pra mais um “lerigou” da mecânica dos fluidos? Vamos buscar esse desenho lá da figura 10.7
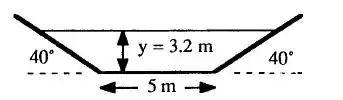
Como é uma seção trapezoidal, duas fórmulas já têm que vir automaticamente na sua cabeça!! A da área normal ao escoamento e do perímetro associado ao escoamento:
Onde
Por que disso? Porque vamos usar a equação de vazão normal que é:
No livro, ele nos dá que para uma superfície de barro, esse coeficiente de rugosidade “n” tem valor de 0,014.
Passo 2
Resposta
Exercícios de Livros Relacionados
Considere o escoamento uniforme através de um canal retangular largo. Se a inclinação do fundo aumentar, a profundidade do escoamento (a) aumentará, (b) diminuirá ou (c) permanecerá constante.
Mostre que para o escoamento critico uniforme, a relação geral de inclinação critica S c = g n 2 y c a 2 R h 4 3 se reduz a S c = g n 2 a 2 y c 1 3 para o escoamento de filme com b y c .
Considere o escoamento uniforme através de um canal aberto recoberto com tijolos e com coeficiente de Manning de n = 0,015 . Se o coeficiente de Manning dobrar ( n=0,030 ) como resultado do cresciment
Água escoa de modo uniforme a meia carga em um canal circular com 2m de diâmetro que é assentado com um declive de 1 , 5m / k m . Se o canal for feito de concreto polido, determine a vazão da água.
Repita o Problema 13-36 para uma vazão de 30m 3 / s .