Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 4.Problemas - Ex. 78
Em áreas onde a temperatura do ar permanece abaixo de por longos períodos de tempo, o congelamento da água nas canalizações subterrâneas é uma grande preocupação. Felizmente, o solo permanece relativamente quente durante esses períodos, e leva semanas para que as temperaturas fiquem negativas perto dos dutos de fornecimento de água dentro do solo. Assim, o solo efetivamente serve como isolante para proteger a água das temperaturas atmosféricas negativas no inverno.
Um terreno em determinado local está coberto com uma camada de neve a durante o período contínuo de , e as propriedades médias do solo local são e . Pressupondo uma temperatura inicial uniforme de para o solo, determine a profundidade mínima em que os dutos de água devem ser enterrados para evitar o congelamento da água.
Passo 1
Caraca, que enunciado enorme! Deu até medo né?! Mas pode vir comigo que vai dar bom! A primeira coisa que a gente tem que fazer é assumir hipóteses. Nessa questão, temos como assumir que:
- Como a temperatura no solo é afetada pelas condições térmicas em apenas uma superfície, o solo pode ser considerado um meio semi-infinito com uma temperatura superficial especificada .
- As propriedades térmicas do solo são constantes. Isso quer dizer que o valor da condutividade térmica e da difusividade térmica são constantes.
Passo 2
Agora vamos para a análise do problema, pessoal! Vou fazer um esquema para vocês para simplificar a visualização dessa questão:
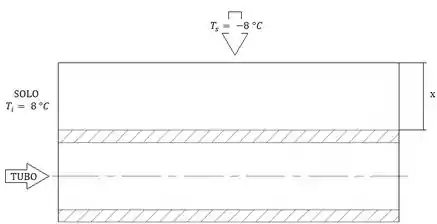
Ufa! Ficou mais fácil de visualizar agora! Bom, temos que determinar a profundidade mínima em que os dutos de água devem ser enterrados para evitar o congelamento da água que é aquele ali!
Passo 3
Como verificamos, este é um problema de condução transiente em meio semi-infinito com uma temperatura superficial especificada constante. Portanto, a distribuição de temperatura em regime transiente unidimensional nesse caso é dada por:
Nós sabemos do enunciado que o terreno está coberto com uma camada de neve a durante o período contínuo de que é considerado um longo período abaixo de ! Portanto, substituindo esses valores na equação, temos:
Da tabela 4-4 a gente descobre que para temos que:
Resposta
Agora ficou fácil né pessoal?! A gente acabou de descobrir que a profundidade mínima em que os dutos de água devem ser enterrados para evitar o congelamento da água é: