Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Operações Unitárias - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 11.Problemas - Ex. 15

Um aspersor de jardim pode ser usado como uma turbina simples. Como mostra a Figura P11.15, o escoamento entra perpendicular ao plano do papel, no centro, e se divide igualmente em Q/2 e Vrel saindo de cada bocal. Os braços giram a uma velocidade angular v e produzem trabalho sobre um eixo. Desenhe o diagrama de velocidades para essa turbina. Desprezando o atrito, encontre uma expressão para a potência fornecida ao eixo. Encontre a rotação para a qual a potência é máxima.

Passo 1

Olhando pra figura que ilustra o problema, a gente pode fazer o seguinte diagrama de velocidades:

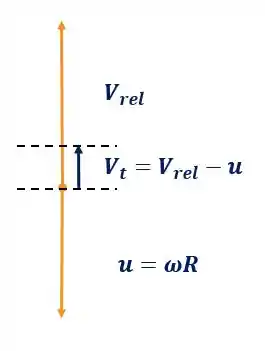
Agora usando a equação de Euler pra potência (Equação 11.11, página 769), temos a seguinte expressão:

P = ρ Q u 2 V t 2 - u 1 V t 1

P = ρ Q u V r e l - u - 0

P = ρ Q ω R V r e l - ω R

Se a gente derivar a potência P em relação à velocidade circunferencial u , a gente chega a:

d P d u = ρ Q ( V r e l - 2 u )

Pra achar a potência máxima, igualamos d P / d u a zero:

ρ Q V r e l - 2 u = 0 →   V r e l = 2 u

Ou seja:

ω = V r e l 2 R

Substituindo na equação pra potência:

P m á x = ρ Q u 2 u - u = ρ Q ω R ²

Resposta

A potência máxima é dada pela equação P m á x = ρ Q ω R ² , pra uma rotação de ω = V r e l 2 R

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a “turbina aspersora” da Figura P11.15, seja R =18 cm, com uma vazão total de 14 m3/h de água a 20 °C. Se o diâmetro de saída do bocal for de 8 mm, calcule(a) a potência máxima fornecida em W e (
Uma bomba centrífuga tem d1 = 178 mm, d2 = 330 mm, b1 = 102 mm, b2 = 76 mm, β1 = 25°, β2 = 40° e gira a 1.160 rpm. Se o fluido for gasolina a 20 °C e o escoamento entra radialmente nas pás, calcule os
Um jato com velocidade V incide em uma pá que se move para a direita com a velocidade Vc, como mostra a Figura P11.18. A pá tem um ângulo de desvio θ. Deduza uma expressão para a potência fornecida à
Uma bomba centrífuga tem r2 = 229 mm, b2 = 51 mm, b2 = 35° e gira a 1.060 rpm. Se ela produz uma altura de carga de 55 m, determine para as condições teóricas: a) a vazão em l/s e (b) a potência. Admi