Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Operações Unitárias - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 11.Problemas - Ex. 17

Uma bomba centrífuga tem d1 = 178 mm, d2 = 330 mm, b1 = 102 mm, b2 = 76 mm, β1 = 25°, β2 = 40° e gira a 1.160 rpm. Se o fluido for gasolina a 20 °C e o escoamento entra radialmente nas pás, calcule os valores teóricos de (a) vazão em l/s, (b) potência e (c) altura de carga em m.

Passo 1

E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!

Nessa questão, temos uma bomba centrífuga com diâmetros interno e externo do rotor de d 1 = 0,178   m e d 2 = 0,330   m , respectivamente. As larguras da pá na entrada e na saída são, respectivamente, b 1 = 0,102   m e b 2 = 0,076   m .

Além disso, os ângulos das pás do rotor são β 1 = 25 ° e β 2 = 40 ° . O rotor gira a uma velocidade angular de eixo de ω = 1160   r p m = 121,47   r a d / s .

O enunciado nos pede então pra calcular a vazão teórica Q , a potência teórica P h e altura de carga teórica H .

Nos próximos passos eu vou te ensinar a calcular tudo isso, mas antes de ir pro Passo 2, mas antes nós temos que lembrar que a massa específica da gasolina a 20 ° C é ρ = 680   k g / m ³ .

Agora sim, vem comigo pra gente matar esse problema juntos!

Passo 2

Pra começar a questão, vamos resolver a letra (a) e achar a vazão teórica Q .

Pra isso, dê uma olhada no diagrama de velocidades de entrada, considerando que a velocidade radial V n 1 é igual à velocidade absoluta V 1 , e o escoamento entra exatamente normal ao rotor:

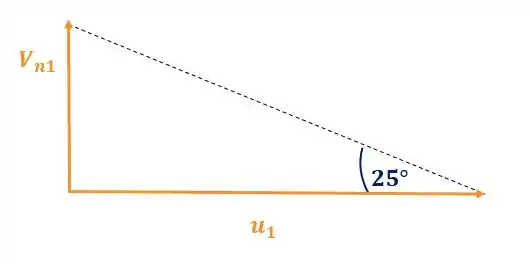
Em primeiro lugar, vamos calcular a velocidade circunferencial u 1 :

u 1 = ω r 1 = 121,47   r a d / s 0,089   m = 10,81   m / s

Agora podemos calcular V n 1 utilizando u 1 :

V n 1 = u 1 tan ⁡ β 1 = 10,81   m / s tan ⁡ 25 ° = 5,04   m / s

Por fim, usando a Equação 11.15, fornecida na página 770, podemos calcular a vazão teórica:

V n 1 = Q 2 π r 1 b 1

5,04   m / s = Q 2 π 0,089   m 0,102   m

Q = 0,287   m 3 / s = 287   L / s

Passo 3

Agora, vamos resolver a letra (b) e calcular a potência teórica P h .

Primeiro, devemos diagrama de velocidades na saída do rotor:

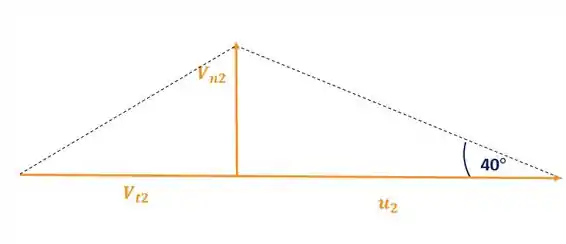
Pra começo de conversa, vamo usar novamente a Equação 11.15 pra calcular a velocidade radial V n 2 :

V n 2 = Q 2 π r 2 b 2 = ( 0,287   m 3 / s ) 2 π 0,165   m 0,076   m = 3,64   m / s

Da mesma forma que no Passo 2, também vamos calcular a velocidade circunferencial na saída:

u 2 = ω r 2 = 121,47   r a d / s 0,165   m = 20,04   m / s

E agora, a gente usa esses dois resultados pra calcular a componente tangencial da velocidade de saída V t 2 :

V t 2 = u 2 - V n 2 cot ⁡ β 2 = 20,04   m / s - 3,64   m / s cot ⁡ 40 ° = 15,7   m / s

Por fim, a gente usa a velocidade tangencial pra calcula a potência teórica P h usando a Equação 11.17 (página 771):

P h = ρ Q u 2 V t 2

P h = 680   k g / m ³ 0,287   m 3 / s 20,04   m / s 15,7   m / s

P h = 61403   W

Passo 4

Pra finalizar a questão, vamo resolver a letra (c) e calcular a carga teórica H que o rotor fornece à gasolina.

Pra isso, vamos usar a Equação 11.3, dada na página 767:

P h = ρ g Q H

61403   W = 680   k g / m ³ 9,81   m / s ² 0,287   m 3 / s H

H = 32,07   m

Pronto, matamos a questão juntos!

Resposta

(a) Q = 287   L / s

(b) P h = 61403   W

(c) H = 32,07   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A Figura P11.24 mostra os dados de desempenho para a bomba modelo 4013 da Taco, Inc.. Calcule a razão entre a altura de carga obtida experimentalmente com vazão nula e o valor ideal U2/g para os sete
Foi pedido para você considerar uma bomba geometricamente semelhante a uma bomba Taco de 9 pol de diâmetro da Figura P11.34 para fornecer 75,7 l/s a 1.500 rpm. Determine os valores apropriados para (a
No Problema P11.31, a vazão no PMR da bomba é 126,2 l/s, o diâmetro do rotor é 406 mm e a rotação é 1.200 rpm. Altere o tamanho dessa bomba com as leis de semelhança para encontrar (a) o diâmetro e (b
Considere as duas bombas dos Problemas P11.28 e P11.35. Se os diâmetros não forem alterados, qual é a melhor para fornecer água a 189,3 l/s, com uma altura de carga de 122 m? Qual é a rotação apropria
Faça um gráfico das curvas de desempenho adimensionais para a bomba do Problema P11.35 e compare com a Figura 11.8. Encontre o diâmetro apropriado em mm e a rotação em rpm para uma bomba geometricamen