Um aspersor de jardim com três braços idênticos é usado para molhar um jardim, girando cm um plano horizontal pelo impulso causado pelo escoamento da água. A água entra no aspersor ao longo do eixo de rotação a uma taxa de 40 L/s e sai dos bocais de 1,2 cm de diâmetro na direção tangencial. O rolamento aplica um torque retardador de Tq = 50 N.m devido ao

atrito das velocidades operacionais previstas. Para uma distância normal de 40 cm entre o eixo de rotação e o centro dos bocais, determine a velocidade angular do eixo do aspersor

Para a gente começar, vamos fazer um dessenho do aspersor visto de cima! Beleza?

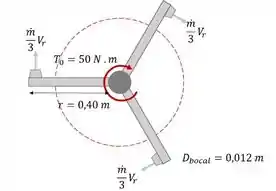
A água entra no aspersor e sai por 3 bocáis idênticos, considerando que a massa se conserva, podemos dizer que:

Agora, se a gente considerar o escoamento incompressível:

Sabendo disso, podemos achar a velocidade do jato, que é a velocidade causada pelo impulso da água:

Beleza!?

Nosso escoamento é permanente, então podemos considerar a seguinte equação do momento angular:

Sabendo que é:

Belezinha! Agora vamos analizar o torque! Aqui tudo que é anti-horário é positivo, ok??

Ou a gente poderia dizer também:

Esse aqui é a velocidade relativa, entre a velocidade do impulso dado pela água e a velocidade velocidade angular do eixo do aspersor, escrevendo, temos:

Ahh, essa velocidade é a tangencial! Pra finalizar, precisamos convertar para velocidade angular:

Agora bora colocar a mão na massa!!!!