Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 6.Problemas - Ex. 49
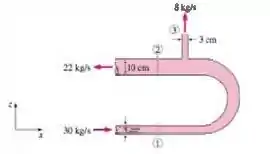
A água escoa e é descarregada de uma seção de tubo em U, como mostra a Figura . No flange (1), a pressão absoluta total é 200 kPa e 30 kg/s escoam para dentro do tubo. No
flange (2), a pressão total é 150 kPa. No local (3), 8 kg/s de água são descarregados para a atmosfera, que está a 100 kPa. Determine as forças totais x e z nos dois flanges que conectam o tubo. Discuta o significado da força da gravidade para este problema. Tome o fator de correção do fluxo do momento como 1,03.
Passo 1
Pra começar, vamos pegar o desenho do enunciado e montar um esqueminha com as forças que estão agindo nesse problema!!
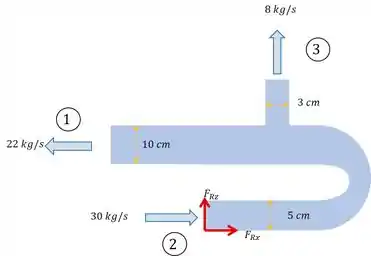
Nesse caso a gente tem um escoamento bidimensional, vamos consideirar o eixo e o eixo . Temos aqui um A equação do momento do escoamento unidimensional permanente:
Ué, mas se a equação é para um escoamento unidimensional e o nosso é bidimensional, como a gente vai fazer?!
Calminha! A gente vai usar essa expressão duas vezes, uma para cada dimensão! Vai ficar assim:
Belezinha!?
Com as informações que o enunciado deu, conseguimos calcular as velocidades em , , . Lembrando que sim, mesmo sendo apenas um escoamento e ele sendo permanente, as velocidades nesses pontos vão ser diferentes, pois os diâmetros são diferentes! Para calcular essas velocidades vamos usar:
Depois de calcular as velocidades é só colocar todas as informações nas fórmulas e calcular!!
Ahh, lembrando de converter as unidades:
E as pressões na fórmula são manométricas, o enunciado deu a pressão absoluta, logo vamos precisar subtrair a pressão em cada ponto pela pressão manométrica, beleza??
Passo 2
Vamos calcular as velocidades:
Agora podemos calcular as forças, começando por :
Vamos dar uma arrumadinha:
Agora é substituir, repara bem que na pressão e a gente ta diminuindo a pressão atmosférica, que é .
Ou:
Esse sinal negativo ai siguinifica que na hora que a gente montou nosso esqueminha a gente assumiu as direções erradas de entrada e saída do escoamento!!
Agora vamos calcular :
Arrumando:
Substituindo e calculando:
Prontinho!!