Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 6.Problemas - Ex. 41

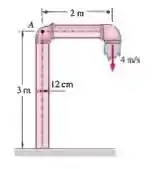
A água escoa através de um tubo com 12 cm de diâmetro que consiste em uma seção vertical com 3 m de comprimento e horizontal com 2 cm de diâmetro com um cotovelo de 90° na saída para forçar a água a ser descarregada para baixo na direção vertical, como mostra a Figura. A água é descarregada no ar atmosférico a uma velocidade de 4 m/s e a massa da seção do tubo quando preenchido com água é de 15 kg por metro linear. Determine o torque que age na iniersecção das seções vertical e horizontal do tubo (ponto A). Qual seria sua resposta se o escoamento fosse descarregado para cima em vez de para baixo?

Passo 1

Para começar, vamos desenhar o diagrama de corpo livre pro primeiro caso, quando o escoamento esta para baixo!

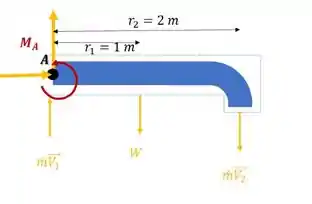
Nesse diagrama a gente tem delimitado o nosso volume de controle e as forças que estão agindo sob ele! W é a força peso que esta agindo no meio do tubo e ele produz um torque em relação a A , assim como m ˙ V 1 → , m ˙ V 2 → produz um torque na saída.

Tudo que é anti-horário é positivo e tudo o que é horário é negativo, beleza?

Temos um escoamento permanente, então a equação de momento fica:

∑ M = ∑ s a í d a r m ˙ V - ∑ E n t r a d a r m ˙ V

Aplicando o que vimos no diagrama de corpo livre, ficamos com:

M A - r 1 W = - r 2 m ˙ V 2

Agora só uma coisinha antes de finalmente colocarmos a mão na massa! Precisamos nos atentar em algumas coisinhas!

m 1 ˙ = m 2 ˙ = m ˙

V 1 ˙ = V 2 ˙ = V ˙

Isso porque o diâmetro do tubo é constante no nosso volume de controle! E façando de diâmetro...

D T = 12   c m = 0,12   m

Agora bora lá!!!

Passo 2

Vamos calcular M A :

M A - r 1 W = - r 2 m ˙ V 2

Para isso precisamos de m ˙   e   W :

m ˙ = ρ π D T 2 4 V

Estamos falando de água, então ρ = 1000   k g / m 3

m ˙ = 1000 × π 0,12 2 4 × 4 = 45,24   k g / s

Agora W :

W = m g

Não temos m , mas o enunciado diz que a massa da seção do tubo quando preenchido com água é de 15 kg por metro linear, então:

m = 15 k g m × 2   m

Agora vamos calcular W :

W = 30 × 9,81 m s 2 = 294 ,   3 K g × m 2 s  

Ou:

W = 294,3   N / m  

Agora podemos achar M A :

M A - ( 1 × 294,3 ) = - ( 2 × 45,24 × 4 )

M A = 70   N . m

Passo 3

Agora a suposição é que a o escoamento seja para cima, mais ou menos assim:

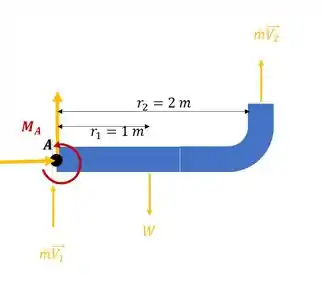
Vamos desconsiderar os efeitos da água caindo, beleza?!

Então o que vai mudar aqui é que m ˙ V 2 → ta pra cima, logo aqui ele vai produzir um momento positivo:

M A - r 1 W = r 2 m ˙ V 2

Substituindo:

M A - ( 1 × 294,3 ) = ( 2 × 45,24 × 4 )

M A = 659   N . m

Tcharaaaam! Resolvido!

Resposta

M A = 70   N .   m

Seo escoamento fosse descarregado para cima em vez de para baixo M A se tornaria:

M A = 659   N . m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um regador comum de gramados pode girar no plano horizontal, conforme mostrado. Água entra verticalmente pelo pivô central com uma vazão Q = 15L / m i n . A água é descarregada em jatos através dos do
No Problema 4.195, calcule a aceleração inicial do regador a partir do repouso, considerando que não haja torque externo aplicado e que o momento de inércia do cabeçote de irrigação é de 0,1k g ⋅ m 2
Líquido, em um jato fino de largura w e espessura h , escoa de uma ranhura e atinge uma placa plana estacionária. Experiências mostram que a força resultante do jato de líquido sobre a placa não atua
Um tubo simetricamente em duas pernas de comprimento L, e o sistema todo gira com velocidade angular ω em torno do seu eixo de simetria. Cada perna é inclinada de um ângulo α em relação ao eixo de rot
Um pequeno regador de gramados é mostrado (Problema 4.196). Ele opera com uma pressão manométrica na entrada de 140k P a . A vazão total em volume de água através do regador é de 4,0L / m i n . Cada j