Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 199

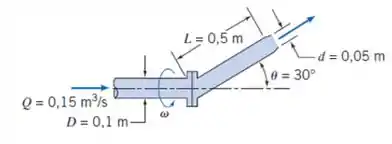
Água escoa com vazão de 0,15   m 3 / s através de uma tubulação com bocal que gira com velocidade constante de 30   r p m . As massas do tubo inclinado e do bocal são desprezíveis comparadas com a massa de água no interior. Determine o torque necessário para girar o conjunto e os torques de reação no flange.

Passo 1

Equação:

r × F s + ∫ V C r × g ρ d ∀ + T e i x o - ∫ V C r × 2 ω × V + ω × ω × r + ω × r ρ d ∀ = ∂ ∂ t ∫ V C r × V ρ d ∀ + ∫ S C r × V   ρ V d A

Considerações Iniciais:

  1. Fluxo Constante;
  2. Escoamento Estacionário;
  3. Cancelamento do torque no corpo;
  4. F S = 0 ;
  5. r × V = 0 ;
  6. Aceleração Angular nula.

Passo 2

Realizando as considerações:

T e i x o - ∫ V C r × 2 ω × V + ω × ω × r ρ d ∀ = 0

T e i x o = ∫ V C r × 2 ω × V + ω × ω × r ρ d ∀

Temos que:

r = L s e n   θ î + cos ⁡ θ k ^ ;

V = V ( s e n   θ î + cos ⁡ θ k ^ ) .

Assim, os termos da equação ficam:

ω × r = ω k ^ × l s e n   θ î + cos ⁡ θ k ^ = ω l   s e n   θ j ^

ω ω × r = ω k ^ × ω l   s e n   θ j ^ = - ω 2 l   s e n   θ î

r × ω × ω × r = l s e n   θ î + cos ⁡ θ k ^ × - ω 2 l   s e n   θ î = - ω 2 l 2   s e n   θ cos ⁡ θ k ^

E

2 ω × V = 2 ω k ^ × V s e n   θ î + cos ⁡ θ k ^ = 2 V ω   s e n   θ j ^

r × 2 ω × V = l s e n   θ î + cos ⁡ θ k ^ × 2 V ω   s e n   θ j ^ = 2 V ω l   S e n 2 θ k ^ - 2 V ω l cos ⁡ θ s e n   θ î

Passo 3

Substituindo os temos na equação:

T e i x o = ∫ V C 2 V ω l   S e n 2 θ k ^ - 2 V ω l cos ⁡ θ s e n   θ î + - ω 2 l 2   s e n   θ cos ⁡ θ k ^ ρ   d ∀

T e i x o = ∫ 0 L 2 V ω l   S e n 2 θ k ^ - 2 V ω l cos ⁡ θ s e n   θ î + - ω 2 l 2   s e n   θ cos ⁡ θ k ^ ρ A   d l

Integrando:

T e i x o = ρ A [ V ω L 2   s e n 2 θ   k ^ - V ω L 2 cos ⁡ θ s e n   θ î + - ω 2 L 3 3 s e n θ cos ⁡ θ j ^

Queremos T e i x o z :

T z = ρ A V ω L 2   s e n 2 θ  

Sendo:

V = Q A

Temos:

T z = ρ Q ω L 2   s e n 2 θ  

Passo 4

Sendo:

ρ = 1000   k g / m 3 ;

Q = 0,15   m 3 / s ;

ω = 2 π N 60 = 2 π ⋅ 30 60 = 3,14   r a d / s ;

L = 0,5   m ;

θ = 30 ° .

Temos:

T z = 1000 ⋅ 0,15 ⋅ 3,14 ⋅ 0,5 2 ⋅ s e n 2   30 ° = 29,44   N ⋅ m  

Passo 5

Podemos escrever também:

M x î + M y j ^ + T z k ^ = ρ A [ V ω L 2   s e n 2 θ   k ^ - V ω L 2 cos ⁡ θ s e n   θ î + - ω 2 L 3 3 s e n θ cos ⁡ θ j ^

Assim, temos que:

M x = - ( - ρ A V ω L 2 cos ⁡ θ s e n   θ ) = ρ Q ω L 2 cos ⁡ θ s e n   θ

E

M y = - - ρ A ω 2 L 3 3 s e n θ cos ⁡ θ = ρ A ω 2 L 3 3 s e n θ cos ⁡ θ

Passo 6

Sendo:

ρ = 1000   k g / m 3 ;

Q = 0,15   m 3 / s ;

ω = 2 π N 60 = 2 π ⋅ 30 60 = 3,14   r a d / s ;

L = 0,5   m ;

θ = 30 ° ;

A = π D 2 4 = π ⋅ 0,1 2 4 = 7,85 x 10 - 3   m 2 .

Temos:

M x = 1000 ⋅ 0,15 ⋅ 3,14 ⋅ 0,5 2 ⋅ cos ⁡ 30 ° ⋅ s e n   30 ° = 50,99   N ⋅ m

M y = 1000 ⋅ 7,85 x 10 - 3 ⋅ 3,14 2 ⋅ 0,5 3 ⋅ 1 3 ⋅ s e n   30 ° cos ⁡ 30 ° = 1,40   N ⋅ m

Resposta

T z = 29,44   N ⋅ m

M x = 50,99   N ⋅ m

M y = 1,40   N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma placa retangular uniforme, com 40 cm de comprimento e 30 cm de profundidade na direção normal ao papel, está suspensa no ar através de uma dobradiça na sua parte superior (no lado de 30 cm). Ela é
O tanque abaixo pesa 500 N vazio e contém 600 litros de água a 20°C. Os tubos 1 e 2 tem diâmetros iguais e 6 cm e vazões permanentes iguais de 300 m³/h. Qual deve ser a leitura P da balança em N?
Quando o escoamento em um tubo se alarga bruscamente de A1 para A2, como mostrado abaixo, aparecem turbilhões de baixa velocidade e baixo atrito nos cantos, e o escoamento gradualmente se alarga até A
Quando imerso em uma corrente uniforme, um cilindro elíptico rombudo cria uma grande esteira a jusante, como idealizado abaixo. A pressão nas seções de montante e de jusante são aproximadamente iguais
Suponha que um defletor é estendido na saída do motor a jato do problema 3.50, como mostrado na figura abaixo. Qual será agora a força de reação Rx sobre a bancada de testes? Será essa reação suficien