Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 68
Um avião voa com velocidade constante Vavião (Figura P9-68). Discuta as condições de contorno de velocidade do ar adjacente à superfície do avião com base em dois sistemas de referência (a) estando no solo e (b) movendo-se com o avião. Da mesma forma, quais as condições de contorno do campo de velocidade afastado no ar (bem longe do avião) em ambos os sistemas de referência?
Passo 1
Pra resolver a letra (a) dessa questão, a gente tem que analisar o avião a partir de um referencial fixo.
Pra você entender melhor, é como se a gente estivesse no chão e visse o avião passar, como na imagem abaixo:
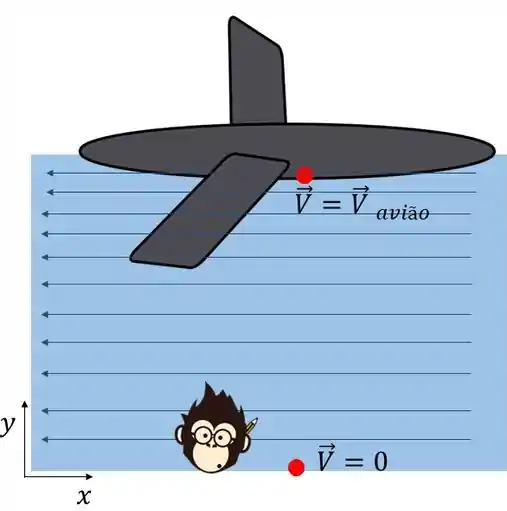
Pela ilustração, dá pra gente sacar que, no nosso ponto de vista parados no solo, é como se o ar estivesse escoando pela perturbação originada do movimento do avião.
Com isso, a gente teria uma condição de contorno de adjacente a qualquer superfície do avião, garantindo a condição de não escorregamento, na qual qualquer fluido adquire a velocidade da superfície onde está escoando.
Da mesma maneira, para distâncias muito grandes do avião, o ar está parado, e assume uma velocidade .
Passo 2
Pra finalizar a questão, a gente tem que resolver a letra (b) analisando o avião como nosso referencial. Seria algo como um volume de controle móvel.
Pra você entender melhor, é como se a gente estivesse dentro do avião, como na imagem abaixo:
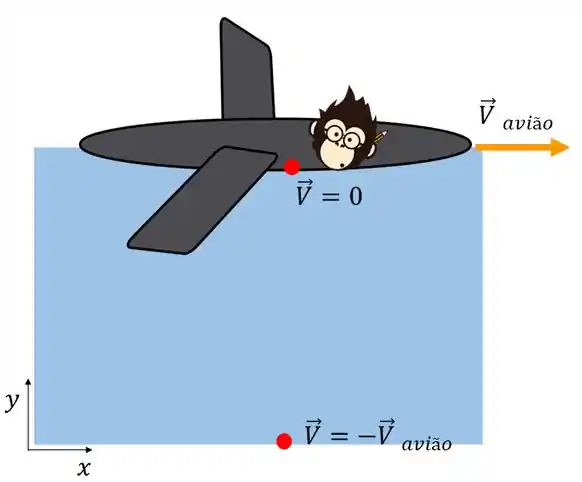
Pela imagem, a gente consegue sacar que, no nosso ponto de vista dentro do avião, é como se a gente estivesse parado e o ar se movendo atrás da gente.
Com isso, a gente teria uma condição de contorno de adjacente a qualquer superfície do avião, garantindo a condição de não escorregamento, na qual qualquer fluido adquire a velocidade da superfície onde está escoando.
Da mesma maneira, para distâncias muito grandes do avião, a gente tem a percepção que o ar está se movendo na direção contrária à nossa, assumindo uma velocidade .
Agora sim, matamos essa questão juntos!
Resposta
(a) Na superfície do avião, a condição de contorno é de . Para distâncias muito grandes do avião, .
(b) Na superfície do avião, a condição de contorno é de . Para distâncias muito grandes do avião, .