Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 9.Exercício - Ex. 9

Água escoa sob uma placa plana de 10   c m de comprimento e 20   c m de largura, com uma velocidade de 0,1   m / s . Determinar a força de arrasto que age na placa. ( ν = 10 - 6 m 2 / s   e ρ = 1000   k g / m 3

Passo 1

Os dados da questão:

  • Comprimento: L = 10   c m = 0,1   m .
  • Largura: B = 20   c m = 0,2   m .
  • Viscosidade: ν = 10 - 6   m 2 / s .
  • Densidade do fluido: ρ = 1000   k g / m 3 .
  • Velocidade do fluido v = 0,1   m / s .

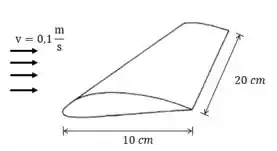
A situação descrita é uma força de arrasto de superfície. Nessa situação podemos calcular o coeficiente de arrasto. Para isso vamos assumir que:

  • O escoamento é perfeitamente laminar sobre a asa.

Passo 2

Considerando que a camada limite é laminar, podemos calcular o arrasto de superfície como:

C a s = 1,328 R e

Substituindo a fórmula do número de Reynolds:

C a s = 1,328 v L ν

C a s = 1,328 ⋅ 10 - 6   m 2 / s 0,1 m s ⋅ 0,1   m

C a s = 1,328 ⋅ 10 - 2

Passo 3

Agora vamos calcular a força de arrasto de superfície:

F a s = C a s ⋅ ρ ⋅ v 0 2 2 A

F a s = C a s ⋅ ρ ⋅ v 0 2 2 L ⋅ B

F a s = 1,328 ⋅ 10 - 2 ⋅ 1000 k g m 3 ⋅ 0,1 m s 2 2 ⋅ 0,1   m ⋅ 0,2   m

F a s = 1,328 ⋅ 10 - 2 ⋅ 1000 k g m 3 ⋅ 0,1 m s 2 2 ⋅ 0,1   m ⋅ 0,2   m

F a s = 1,328 ⋅ 10 - 3   N

Convertendo as unidades ( 1   d i n a   =   10 - 5   N )

F a s = 132,8   d i n a

Resposta

F a s = 132,8   d i n a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma ciclista pode atingir uma velocidade máxima de 30 km/h em um dia calmo. A massa total da ciclista e da bicicleta é 65 kg. A resistência de rolamento dos pneus é F R = 7,5 N, e o coeficiente de arr
Um disco redondo, fino, de raio R, está posicionado normal a uma corrente fluida. As distribuições de pressão sobre as superfícies frontal e posterior são medidas e apresentadas na forma de coeficient
Umônibustrafegaa80km/hnoar­padrão.Aáreafrontaldoveículoé7,5m2eocoeficientedearrastoé0,92.Quantapotênciaé requeridaparasuperaroarrastoaerodinâmico?Estimeamáximavelocidadedoônibus,seomotortempotêncianom
Um aeroplano reboca uma faixa de propaganda acima de um estádio de futebol em uma tarde de sábado. A faixa tem 12 m de altura e 13,7 m de comprimento. Segundo Hoerner [16], o coeficiente de arrasto ba
A componente vertical da velocidade de aterrissagem de um paraquedas deve ser inferior a 6 m/s. A massa total do paraquedas e do paraquedista é 120 kg. Determine o mínimo diâmetro do paraquedas aberto