Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 9.Exercício - Ex. 16

Um papagaio pesa 1 N e tem uma área de 74,4   d m 2 . A tensão na linha é 30 N quando ela forma um ângulo de 45º com a direção do vento. Para um vento de 36 km/h, quais serão os coeficientes de arrasto e sustentação, a fim de que o papagaio forme um ângulo de 30º com a horizontal? ( ρ a r = 1,2   k g / m 3 . Considerar o peso aplicado no centro geométrico e adotar a área projetada como área de referência)

Passo 1

Dados da questão:

  • Peso: P = 1   N
  • Área: A s u p e f i c i e = 74,4   d m 2 = 0,744   m 2
  • Tração: T = 30   N
  • Velocidade do vento: v = 36   k m / h = 10   m / s
  • Ângulo da tração: α = 45 º
  • Ângulo do papagaio: θ = 30 º
  • Densidade do ar: ρ a r = 1,2   k g / m 3

Passo 2

A pegadinha desta questão está na área. A questão nos dá a área superficial, mas como o papagaio está inclinado, a área de referência muda:

A = 0,744   m 2 ⋅ sen ⁡ 30 = 0,372   m 2

Passo 3

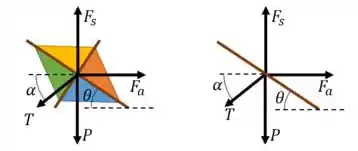
Vamos considerar que o papagaio está estático no ar. Podemos determinar as equações:

∑ F x = 0 ⇒ F a - T ⋅ sen ⁡ α = 0

∑ F y = 0 ⇒ F s - P - T ⋅ cos ⁡ α = 0

Passo 4

Vamos usar o eixo X para calcular o coeficiente de arrasto:

F a - T ⋅ sen ⁡ α = 0

F a = T ⋅ sen ⁡ α

Substituindo a fórmula da força de arrasto

C a ⋅ ρ ⋅ v 2 2 A = T ⋅ sen ⁡ α

C a = 2 ⋅ T ⋅ sen ⁡ α ρ ⋅ v 2 ⋅ A

Aplicando os valores:

C a = 2 ⋅ 30 ⋅ sen ⁡ 45 1,2 k g m 2 ⋅ 10 m s 2 ⋅ 0,372   m 2

C a = 0,95

Passo 5

Vamos usar o eixo Y para calcular o coeficiente de sustentação:

F s - P - T ⋅ cos ⁡ α = 0

F s = P + T ⋅ cos ⁡ α

Substituindo a fórmula da força de arrasto

C s ⋅ ρ ⋅ v 2 2 A = P + T ⋅ cos ⁡ α

C s = 2 ( P + T ⋅ cos ⁡ α ) ρ ⋅ v 2 ⋅ A

Aplicando os valores:

C s = 2 ( P + T ⋅ cos ⁡ α ) ρ ⋅ v 2 ⋅ A

C s ≈ 1

Resposta

C a = 0,95

C s = 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um lançador de beisebol arremessa uma bola a 128k m / h . A base está a 18,3 m da plataforma de lançamento. Que rotação deve ser aplicada à bola para desvio horizontal máximo de uma trajetória retilín
Uma bola de golfe (diâmetro D=43m m ) com cavidades circulares é golpeada e sai com velocidade de 20m / s e giro anti-horário (backspin) de 2000 rpm. A massa da bola é 48g . Avalie as forças de susten
Um modelo de aerofólio com corda de 150 mm e envergadura de 750 mm é colocado em um túnel de vento com um escoamento de ar igual a 300 m/s (o ar está a 20°C). O modelo é montado sob uma haste suporte
Um avião está em voo de cruzeiro a 225 km/h no ar padrão. O coeficiente de sustentação para esta velocidade é 0,45 e o coeficiente de arrasto é 0,065. A massa do avião é 900 kg. Calcule a área efetiva
A área total efetiva dos hidrofólios de um barco anfíbio é 0,7m 2 . Seus coeficientes de sustentação e arrasto são 1,6 e 0,5, respectivamente. A massa total da embarcação em condição de navegação é 18