Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 38
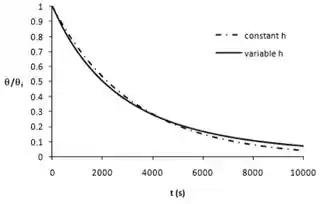
Um bastão longo de alumínio altamente polido, com diâmetro , está pendurado verticalmente em uma grande sala. A temperatura inicial do bastão é e o ar da sala está a . No instante , a temperatura do bastão é e no instante , a temperatura do bastão é . Determine o valor das constantes e que aparecem na Equação 5.26. Represente graficamente a temperatura do bastão versus o tempo para . No mesmo gráfico, represente a temperatura do bastão versus o tempo para um valor constante do coeficiente de transferência de calor, calculado a uma temperatura do bastão de . Em todos os casos, avalie as propriedades em .
Passo 1
Vamo lá galera! Se o coeficiente de transferência de calor é dado pela Equação 5.26, então a temperatura em função do tempo é dada pela Equação 5.28:
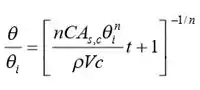
onde e é a área exposta à convecção, . Como a temperatura da haste é conhecida em dois momentos diferentes, a Equação (1) pode ser avaliada nestes dois momentos, tornando possível resolver para as duas incógnitas, e . As duas equações são
Passo 2
Estas equações não podem ser resolvidas explicitamente para C e n. Elas podem ser resolvidas numericamente nesta forma, usando IHT ou algum outro software, ou podem ser ainda mais manipuladas para resolver para os tempos:
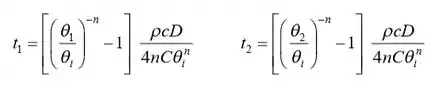
Tomando a razão de Equações,
Passo 3
Isto pode ser resolvido iterativamente ou numericamente para n, para encontrar n = 0,25. Então C pode ser determinado pela Equação (3a) ou (3b):
O gráfico abaixo mostra a temperatura da haste em função do tempo usando a Equação (1) acima para coeficiente variável de transferência de calor, bem como a temperatura da haste assumindo o valor constante de , usando o texto da Equação 5.6.
