Uma parede plana de espessura e condutividade térmica experimenta uma taxa volumétrica de geração uniforme . Como mostrado no esboço como Caso 1, a superfície em é perfeitamente isolada, enquanto a outra superfície é mantida a uma temperatura constante e uniforme . Para o Caso 2, uma fita dielétrica muito fina é inserida no plano central da parede para isolar eletricamente as duas seções, e . A resistência térmica da fita é . Os parâmetros associados à parede são: , , e .

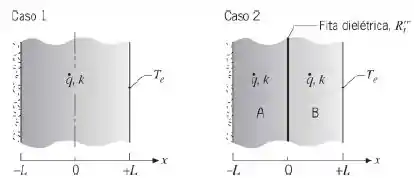
(a) Esboce a distribuição de temperaturas para o Caso 1 em coordenadas . Descreva as características principais dessa distribuição. Identifique a localização da temperatura máxima na parede e calcule essa temperatura.

(b) Esboce a distribuição de temperaturas para o Caso 2 nas mesmas coordenadas . Descreva as características principais dessa distribuição.

(c) Qual é a diferença de temperaturas entre as duas paredes em no Caso 2?

(d) Qual é a posição da temperatura máxima na parede composta do Caso 2? Calcule essa temperatura.

(a) Queremos nessa questão, esboçar a distribuição de temperatura para o caso 1 nas coordenadas .

No caso 1, temos que a distribuição de temperatura é parabólica, ou seja, a equação geral para transferência de calor pode ser escrita da seguinte maneira:

Aqui, é a temperatura na direção de , é a taxa de transferência de calor, é a condutividade térmica da parede, é à distância ao longo da parede na direção vertical e e são constantes arbitrárias.

Queremos encontrar e para isso, podemos usar as condições de contorno. A primeira condição se dá ao fato de que a superfície onde a parede está isolada. Ou seja:

Aplicando essa condição, temos o seguinte:

Agora vamos usar a segunda condição de contorno. Quando , temos que . Assim temos que:

Assim, temos que a equação de distribuição de temperatura é:

Substituindo os dados fornecidos na equação acima temos o seguinte:

Com a equação da distribuição de calor encontrada acima, podemos plotar o gráfico da destruição de temperatura. Assim temos:

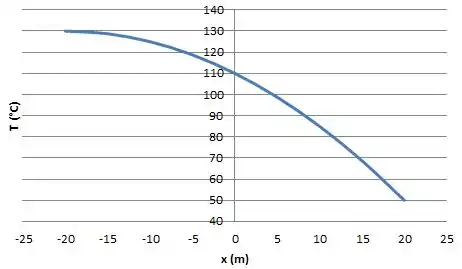
Aqui, a curva é de natureza parabólica, uma vez que o grau de função é 2.

Temos que a temperatura máxima ocorre quando

Pela condição de contorno feita anteriormente, isso ocorre em . A temperatura máxima nesse ponto é

(b) Queremos nessa questão, esboçar a distribuição de temperatura para o caso 2 nas mesmas coordenadas . Um esquema para o caso 2 pode ser o seguinte:

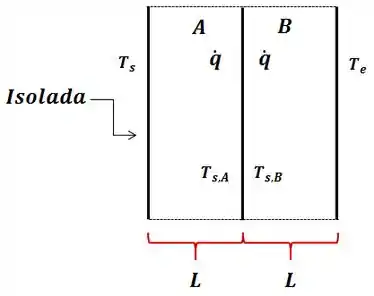
Para isso, vamos calcular as temperaturas , e . Pela suposição de estado estacionário, temos que o fluxo de calor conduzido em A, é igual em B. Assim, podemos dizer que:

Substituindo os termos da equação pelos dados obtidos, temos:

Também podemos dizer que:

Substituindo os termos da equação pelos dados obtidos, temos:

Também podemos dizer que:

Substituindo os termos da equação pelos dados obtidos, temos:

Com as temperaturas encontradas acima, podemos plotar o gráfico da destruição de temperatura. Assim temos:

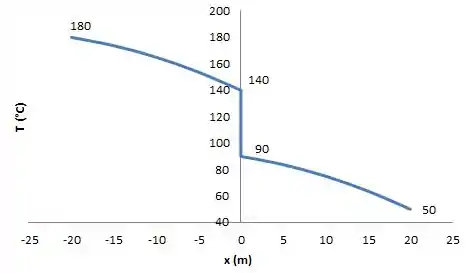
No caso 2, a distribuição de temperatura, , é parabólica em partes, com gradiente zero em e uma descontinuidade na fita dielétrica. Os gradientes de temperatura em ambos os lados da fita dielétrica são iguais.

(c) Queremos a diferença de temperatura entre as duas paredes em para o caso 2. Ou seja:

Pelos dados obtidos nos passos anteriores, temos que a diferença de temperatura é:

Portanto, a diferença de temperatura entre as duas paredes é .

(d) Queremos a localização da temperatura máxima da parede composta no caso 2. Pelo gráfico de feito no item (b), podemos perceber que a temperatura máxima ocorrera em . Temos que nesse ponto a temperatura é .

Portanto, a temperatura máxima na parede composta é .