Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 4.Problemas - Ex. 9
Considere uma esfera e um cilindro de igual volume feitos de cobre. Tanto a esfera quanto o cilindro estão inicialmente á mesma temperatura e expostos à convecção no mesmo ambiente. Qual você acredita que vai esfriar mais rápido: o cilindro ou a esfera? Por quê?
Passo 1
Fala galera!!
Podemos começar analisando o seguinte gráfico do livro:
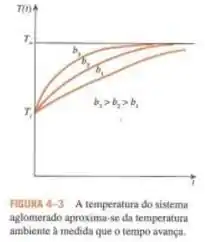
Esse gráfico vem da seguinte equação:
Onde
Aqui, é o coeficiente de transferência de calor, é a área da superfície, é a densidade do material, é o volume do material e é o calor específico.
Vamos supor que, para ambos os materiais, o número de Biot seja menor que . Podemos perceber pelo gráfico que quanto maior o valor de , mais rápido ocorre uma mudança de temperatura. Então, para o cilindro e a esfera de mesmo volume, quem tiver o maior valor de esfriará mais rápido.
Passo 2
Foi dito no enunciado que, a esfera e o cilindro são feitos do mesmo material e tem o mesmo volume, logo, os valores de , , e são iguais. Então a única coisa que irá diferenciar o valor de para os dois é a área superficial. Quem tiver maior área superficial, terá maior valor de , logo, esfriará mais rápido.
Podemos usar a relação de que o volume de uma esfera e cilindro é igual.
Aqui, é o raio da esfera, é o raio do cilindro e é a altura do cilindro. Podemos isolar da seguinte forma:
Podemos escrever como sendo uma proporção da área de superfície da esfera e do cilindro.
Podemos substituir pela relação que encontramos a partir do volume. Assim temos:
Podemos tiver o denominador e o numerador por .
Passo 3
O valor de sempre será menor que para cada valor da razão, desde que os valores de e sejam positivos.
Assim, a área de superfície da esfera será menor que a área de superfície do cilindro e, portanto, o valor de para a esfera será menor que o valor de para o cilindro.
Portanto, o cilindro esfria mais rápido que a esfera.
Resposta
O cilindro esfria mais rápido.