Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 79
Uma esfera de cobre puro, com diâmetro de e uma emissividade de , está suspensa em um grande forno com as paredes a uma temperatura uniforme de . Ar escoa ao redor da esfera a uma temperatura de e a uma velocidade de.
(a) Determine a temperatura da esfera no regime estacionário.
(b) Estime o tempo necessário para a esfera chegar a da temperatura do regime estacionário, se ela estiver a uma temperatura inicial, uniforme, de .
(c) Com o objetivo de diminuir o tempo para aquecer a esfera, a velocidade do ar é dobrada, com todas as outras condições permanecendo as mesmas. Determine a temperatura da esfera no regime estacionário e o tempo necessário para ela atingir uma temperatura a desse valor. Represente no mesmo gráfico o histórico da temperatura da esfera para as duas velocidades.
Passo 1
Aqui nós temos uma peça esférica de cobre puro com um diâmetro de e emissividade de é suspensa em um grande forno com paredes a uma temperatura uniforme de . O fluxo de ar sobre a peça de trabalho tem uma temperatura de com uma velocidade de Ilustrativamente, temos:
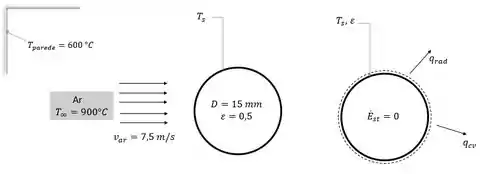
Com isso, queremos encontrar a temperatura em estado estacionário da peça de trabalho e o tempo necessário para que a peça atinja dentro de da temperatura em estado estacionário se a temperatura inicial e uniforme for .
Passo 2
Para resolver essa questão nós vamos assumir que:
(1) O fluxo ocorre sobre uma esfera lisa;
(2) A esfera se comporta como objeto isotérmico no espaço (o método de capacitância concentrada é válido);
(3) A esfera é um objeto pequeno em ambientes isotérmicos grandes;
(4) As propriedades são constantes.
Além disso, vamos utilizar as propriedades do ar da Tabela A.4 nas temperaturas e . Na letra (a) queremos calcular a temperatura da esfera no regime estacionário que é determinado a partir do balanço energético na esfera:
Onde,
Passo 3
O coeficiente de convecção pode ser estimado usando a correlação de Whitaker, , onde todas as propriedades, exceto , são avaliadas em Assumindo para avaliar .
Substituindo os valores e jogando na expressão do balanço de energia, encontramos .
Passo 4
Na letra (b) queremos o tempo necessário para a esfera chegar a da temperatura do regime estacionário, se ela estiver a uma temperatura inicial, uniforme, de . Esse tempo pode ser determinada a partir do balanço energético da condição transiente.
Sabendo que não é constante, mas depende de O tempo para é.