Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 83
Revestimentos de alumínio altamente refletivos podem ser formados na superfície de um substrato pela aspersão da superfície com gotas de alumínio fundido. As gotas são descarregadas de um injetor, deslocam-se através de um gás inerte (hélio) e devem ainda estar no estado líquido no instante da colisão.
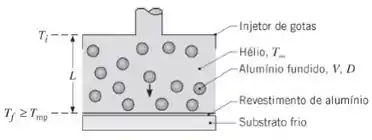
Considere condições nas quais gotas com diâmetro, velocidade e temperatura inicial de , e , respectivamente, atravessam uma camada estagnada de hélio atmosférico que se encontra a uma temperatura de . Qual é a espessura máxima permitida para a camada de hélio para garantir que a temperatura das gotas colidindo com o substrato seja maior ou igual ao ponto de fusão do alumínio As propriedades do alumínio fundido podem ser aproximadas por e
Passo 1
Nessa questão nós temos o diâmetro, a velocidade, a temperatura inicial e o ponto de fusão de gotículas de alumínio fundido. Além da temperatura da atmosfera de hélio.
A partir disso queremos encontrar a separação máxima permitida entre o injetor de gotículas e o substrato. Vamos lá então!
Passo 2
Para resolver essa questão vamos assumir que a aproximação de capacitância amplificada é válida, as propriedades são constantes e a radiação é desprezível. Além disso, vamos retirar os valores da propriedade do hélio da Tabela A.4 para as temperaturas de e .
Temos,
Usando a correlação de Whitaker:
Então,
Passo 3
O tempo de voo para a gota esfriar de a pode ser obtido por:
Substituindo os valores encontramos,
Então, a separação máxima é: