Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 4.Problemas - Ex. 94
Um bloco de gelo cilíndrico () de 2 cm de altura é colocado com a base de 2 cm de diâmetro sobre uma sala a 24 °C. O coeficiente de transferência de calor nas superfícies expostas do bloco de gelo é , e a transferência de calor a partir da base do bloco de gelo na mesa é desprezível. Considerando que o bloco de gelo não começa a derreter em qualquer ponto durante pelo menos 3 horas, determine a temperatura inicial do bloco de gelo.
Passo 1
Vamos analisar o enunciado juntos e entender o que o problema quer de você.
Em primeiro lugar, perceba que as dimensões do cilindro são muito próximas entre si, e não podemos considerar uma transferência de calor unidimensional.
No entanto, como todo o cilindro está imerso no mesmo fluido (ar) e submetido ao mesmo coeficiente de transferência de calor, além de não haver geração, podemos aproximar a resolução desse cilindro multidimensional como o produto das soluções analíticas de um cilindro infinito e uma parede plana
Ou seja:
Além disso, esse problema tem uma “pegadinha”. Mas não se preocupe, eu vou te ensinar como não cair nela em nenhuma outra questão do tipo.
A pegadinha está no fato do cilindro de gelo estar em uma mesa. Preste atenção nessa imagem:
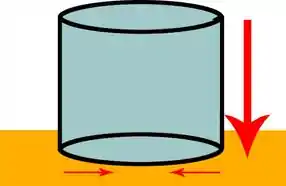
As linhas vermelhas representam o sentido da transferência de calor. Veja que, nos lados do bloco que formam a base, expostos de ambos os lados à convecção, existem um plano de simetria apontando para o centro da base, onde os vetores do fluxo de calor se anulam. Portanto, podemos considerar sua dimensão característica R como sendo o raio do cilindro, ou seja, metade do diâmetro.
Mas preste atenção na dimensão correspondente à altura desse bloco. Como a base está sobre uma mesa onde não há transferência de calor, temos apenas um vetor vindo do ambiente externo. Ou seja, a dimensão característica L deve ser correspondente a toda a altura do bloco, ou nossa análise estaria errada.
Além disso, a questão pede que a gente analise onde o bloco começará a derreter. Bem, ele irá começar a derreter quando algum dos pontos do bloco atingir 0 °C. Além disso, o primeiro lugar onde isso irá ocorrer irá ser na parte superior do bloco e na superfície externa, ou seja, nos lugares onde e .
Ou seja, , onde essas são as dimensões características do bloco.
Agora, pra gente não se perder, vamos guardar as propriedades que vamos usar nos próximos passos:
Passo 2
Agora, devemos calcular os adimensionais (Número de Biot e Número de Fourier) para cada uma das geometrias analisadas.
Vamos lembrar que a dimensão característica para um cilindro infinito é o seu raio (R) e para uma parede plana submetida a convecção em ambos os lados é metade de sua espessura total, que, nesse caso, é a altura do cilindro (2L). Assim:
Primeiro, vamos calcular o Número de Fourier (τ) para as duas geometrias. Vamos lembrar que, segundo o enunciado o processo ocorre em 3 h, ou seja, 10800 . Sendo assim:
Note que ambos os valores de τ foram maiores que 0,2. Isso garante que nosso problema está sendo analisando em tempos muito longos, e podemos aproximar as soluções individuais dos perfis de temperatura para:
Agora, vamos calcular o número de Biot para as duas geometrias:
Iremos agora até a Tabela 4-2 (página 239), onde vamos usar os valores de para ambas as geometrias para encontrar e para as duas:
Já para a parede plana, devemos fazer uma interpolação entre 0,1 e 0,2:
Passo 3
Vamos resolver as soluções unidimensionais.
Primeiro, vamos resolver para o cilindro:
Devemos ir até a Tabela 4-3 (página 239) para encontrar o valor de . Como esse valor não é tabelado, vamos interpolar entre e .
Portanto, . Sendo assim:
Agora, vamos resolver para a parede plana:
Agora, basta multiplicar as soluções para encontrar o resultado para o cilindro curto:
Devemos lembrar, ainda, que
Sendo assim:
Resposta
Ei, a resposta está no passo a passo :)