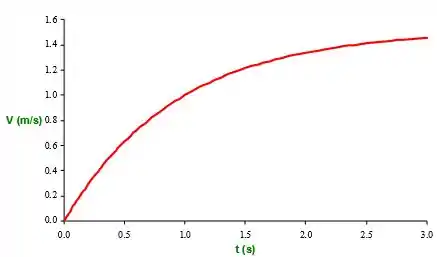
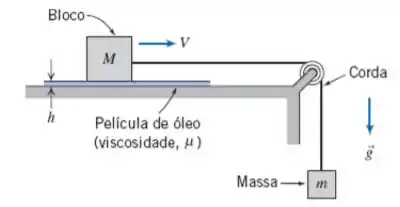
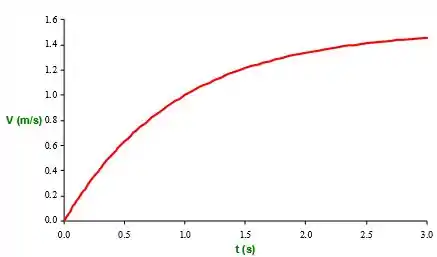
Um bloco de massa M desliza sobre uma fina película de óleo. A espessura do filme é he a área do bloco é A. Quando liberada, a massa m exerce tração na corda, causando a aceleração do bloco. Negligencie o atrito da polia e a resistência do ar. Desenvolva uma expressão algébrica para a força viscosa que atua no bloco quando ele se move na velocidade V. Deduza uma equação diferencial para a velocidade do bloco em função do tempo. Obtenha uma expressão algébrica para a velocidade do bloco em função do tempo. A massa M = 5 kg, m = 1 kg, A = 25 cm2 eh = 0,5 mm. Se o bloco demorar 1 segundo para atingir uma velocidade de 1 m / s, determine a viscosidade, μ, do óleo. Esboce a curva V (t).

Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Por equilíbrio, temos que:

Somando as equações acima:

A força de atrito é dada por:

Logo:

Esta equação diferencial não é tão somples de resolver. Mas como esse não é o foco aqui, vamos pular para o resultado:

Esboçando a curva: