Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 40
A distribuição de velocidade para o escoamento laminar desenvolvido entre placas paralelas é dada por
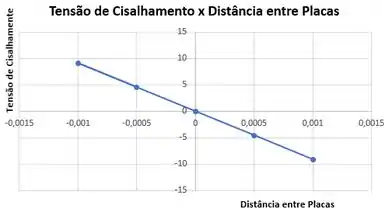
Em que é a distância separando as placas e a origem está situada na linha mediana entre as placas. Considere um escoamento de água a , com e . Calcule a tensão de cisalhamento na placa superior e dê o seu sentido. Esboce a variação da tensão de cisalhamento em uma seção transversal do canal.
Passo 1
Pela definição da Tensão de Cisalhamento, temos:
Assim:
Passo 2
Calculando a tensão de cisalhamento na placa superior e dando o seu sentido:
Sendo:
;
;
;
.
Temos:
Como temos um sinal negativo, temos a força de cisalhamento agindo contrária a direção do escoamento.
Passo 3
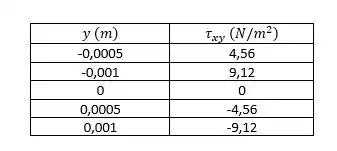
A variação da tensão de cisalhamento em uma seção transversal do canal se dá pela equação:
Com em metros.
Resposta
Exercícios de Livros Relacionados
Uma importante equação na teoria de vibrações é: m d 2 x d t 2 + c d x d t + k x = f ( t ) Em que m (kg) é a massa e x (m) é a posição no instante de tempo t (s). Para uma equação dimensionalmente con
Na Seção 1.6, aprendemos que a equação de Manning nos permite calcular a velocidade de escoamento V (m/s) em um canal feito de concreto mal acabado, dados o raio hidráulico Rh (m), a inclinação S0 do
A vazão mássica de um escoamento de água, determinada pela coleta de descarga em um dado intervalo de tempo, é 0,2 kg/s. A escala usada na medição permite leituras de 0,05 kg e a precisão do cronômetr
Repita o cálculo da incerteza do Problema 1.40 para o ar em um balão de ar quente. Considere que a altura medida no barômetro é 759 mm de mercúrio com uma incerteza de ± 1 mm de mercúrio e a temperatu
Usando as dimensões nominais da lata de refrigerante dadas no Problema 1.47, determine a precisão com que o diâmetro e a altura devem ser medidos para que o volume da lata seja estimado dentro de uma