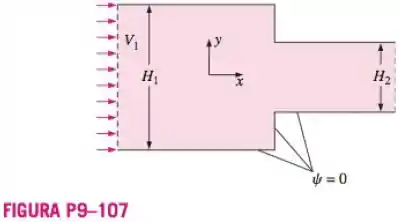
Bob usará um programa de dinâmica de fluidos computacional para modelar o escoamento permanente de um fluido incompressível através de uma contração brusca bidimensional, conforme mostra a Figura P9-107. A altura do canal muda de  para . Deve ser especificada velocidade uniforme  na fronteira esquerda do domínio computacional. O aplicativo de CFD usa um esquema numérico no qual uma função corrente deve ser especificada ao longo de todas as fronteiras do domínio computacional. Conforme mostra a Figura P9-107,  é especificado como zero ao longo de toda a parede inferior do canal. Qual é o valor de  que Bob deverá especificar na parede superior do canal?  Como Bob deve especificar  no lado esquerdo do domínio computacional?  Discuta como Bob pode especificar  no lado direito do domínio computacional.

(a) Para resolver essa questão, é importante saber que a vazão em volume por unidade de largura é igual à diferença entre os valores das duas funções correntes que limitam o canal. Desde que o fluxo seja incompressível em estado estacionário e tenha apenas dois componentes (fluxo bidimensional). Ou seja, pela equação 9-25 temos que:

Temos que a vazão em volume pode ser dada da seguinte maneira:

Substituindo uma relação na outra, temos seguinte:

Aqui, é a velocidade de entrada, é a taxa de fluxo em volume, é a distância entre as camadas superior e inferior, é a largura entre as linhas de vapor superior e inferior, é a função da linha de corrente inferior e é a função da linha de corrente superior do canal.

Agora, vamos substituir os termos da equação encontrada no passo anterior pelos dados fornecidos no enunciado. Assim temos:

Portanto, o valor de  que Bob deve especificar na parede superior do canal é .

(b) Como mencionado anteriormente, temos que o fluxo é uniforme, portanto a variação da função da linha de corrente também é uniforme, ou seja, ela pose ser dado como

em que muda com o aumento da altura. Para o lado esquerdo do domínio computacional, quando temos que e quando temos que . Assim, a função acima pode ser escrita da seguinte maneira:

Aqui, é a altura em qualquer ponto do canal e é a função da linha de corrente para a altura . Substituindo os termos da equação acima pelos dados fornecidos no enunciado, temos o seguinte:

Portanto, Bob deve especificar  no lado esquerdo do domínio computacional como uma função de .

(c) Para resolver a letra , vamos primeiro calcular a velocidade no lado direito do domínio computacional. Supomos que escoamento é estacionário, portanto, podemos dizer que

Aqui, é a velocidade de saída e é a altura após a contração. Substituindo os termos da equação acima pelos dados fornecidos no enunciado, temos o seguinte:

As funções da linha de corrente à esquerda são um produto direto da velocidade no tempo à esquerda e da altura vertical, que é comprovada pela equação encontrada na letra . Da mesma forma, a função da linha de corrente à direita, na saída, é um produto direto da velocidade na saída e da altura na saída.

Portanto, Bob deve especificar  no lado direito do domínio computacional como uma função de .