Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 110

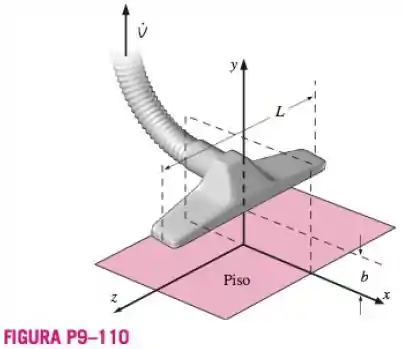
Aproximamos o escoamento do ar para dentro do acessório de piso, de um aspirador de pó por uma função corrente ψ = - V ˙ 2 π L arctan ⁡ sen ⁡ 2 θ cos ⁡ 2 θ + b 2 / r 2   no plano central (o plano  x y ) em coordenadas cilíndricas, onde  L  é o comprimento do acessório,  b  é a altura do acessório acima do piso, e  V ˙  é a vazão em volume do ar que está sendo sugado na mangueira. Na Figura P9-110 é mostrada uma vista tridimensional com o piso no plano  x z ; modelamos uma fatia bidimensional do escoamento no plano  x y  através do eixo central do acessório. Note que tomamos (arbitrariamente)  ψ = 0 ao longo do eixo  x  positivo  ( θ = 0 ) .  a Quais são as dimensões principais da função corrente dada?  b Coloque a função corrente na forma adimensional definindo  ψ * = 2 π L / V ˙ ψ  e  r * = r / b .  c Resolva a sua equação na forma adimensional para r * com uma função de  ψ *  e θ . Use essa equação para desenhar várias linhas de corrente adimensionais do escoamento. Por consistência, faça o gráfico no intervalo - 2 < x * < 2 e 0 < y * < 4 , onde x * = x / b e y * = y / b . (Sugestão: ψ * deve ser negativa para resultar na direção correta do escoamento).

Passo 1

Fala Galera!!

Nessa questão, nos foi fornecidos a seguinte função corrente no enunciado:

ψ = - V ˙ 2 π L arctan ⁡ sen ⁡ 2 θ cos ⁡ 2 θ + b 2 / r 2

Passo 2

(a) Aqui, queremos encorar às dimensões principais da função de corrente, para isso, vai escrever as dimensões de cada termo.

A vazão em volume do ar possuem as seguintes dimensões:

V ˙ = m 3 s - 1 = L 3 t - 1

O comprimento do acessório possuem as seguintes dimensões:

L = m = L

A altura do acessório possuem as seguintes dimensões:

b = m = L

O raio da parte circular do aspirador possuem as seguintes dimensões:

r = m = L

Assim, temos que função arcotangente fica adimensional, logo a função de corrente fica da seguinte forma:

ψ = - V ˙ 2 π L arctan ⁡ sen ⁡ 2 θ cos ⁡ 2 θ + b 2 / r 2 = L 3 t - 1 L

ψ = L 3 t - 1 L

ψ = L 2 t - 1

Portanto, dimensão da função de corrente é L 2 t - 1 .

Passo 3

(b) Agora, queremos colocar função de corrente na forma adimensional, para isso, vamos reorganizar a função da seguinte maneira:

ψ = - V ˙ 2 π L arctan ⁡ sen ⁡ 2 θ cos ⁡ 2 θ + b 2 / r 2

2 π L V ˙ ψ = - arctan ⁡ sen ⁡ 2 θ cos ⁡ 2 θ + b / r 2

2 π L V ˙ ψ = - arctan ⁡ sen ⁡ 2 θ cos ⁡ 2 θ + 1 r / b 2

Substituindo os termos da equação acima pelos termos definidos no enunciado ψ * = 2 π L / V ˙ ψ   e r * = r / b , temos o seguinte:

ψ * = - arctan ⁡ sen ⁡ 2 θ cos ⁡ 2 θ + 1 r * 2

ψ * = - arctan ⁡ sen ⁡ 2 θ cos ⁡ 2 θ + 1 r * 2

Portanto, a forma adimensional da função de corrente é a seguinte:

ψ * = - arctan ⁡ sen ⁡ 2 θ cos ⁡ 2 θ + 1 r * 2

Passo 4

(c) Agora, vamos resolver a forma adimensional da função de corrente encontrada no passo anterior a fim de encontrar r * em função de ψ *  e θ . Para isso, podemos aplicar a função tangente dos dois lados da equação. Assim temos:

ψ * = - arctan ⁡ sen ⁡ 2 θ cos ⁡ 2 θ + 1 r * 2

- ψ * = arctan ⁡ sen ⁡ 2 θ cos ⁡ 2 θ + 1 r * 2

tan ⁡ - ψ * = tan ⁡ arctan ⁡ sen ⁡ 2 θ cos ⁡ 2 θ + 1 r * 2

tan ⁡ - ψ * = sen ⁡ 2 θ cos ⁡ 2 θ + 1 r * 2

cos ⁡ 2 θ + 1 r * 2 = sen ⁡ 2 θ tan ⁡ - ψ *

1 r * 2 = sen ⁡ 2 θ tan ⁡ - ψ * - cos ⁡ 2 θ

1 r * 2 = sen ⁡ 2 θ - cos ⁡ 2 θ tan ⁡ - ψ * tan ⁡ - ψ *

r * 2 = tan ⁡ - ψ * sen ⁡ 2 θ - cos ⁡ 2 θ tan ⁡ - ψ *

r * = ± tan ⁡ - ψ * sen ⁡ 2 θ - cos ⁡ 2 θ tan ⁡ - ψ *

Portanto, a equação adimensional para  r * em função de ψ *  e θ é:

r * = ± tan ⁡ - ψ * sen ⁡ 2 θ - cos ⁡ 2 θ tan ⁡ - ψ *

Passo 5

Agora podemos plotar o gráfico com as linhas de fluxo adimensionais da seguinte maneira:

Resposta

(a)

ψ = L 2 t - 1

(b)

ψ * = - arctan ⁡ sen ⁡ 2 θ cos ⁡ 2 θ + 1 r * 2

(c)

r * = ± tan ⁡ - ψ * sen ⁡ 2 θ - cos ⁡ 2 θ tan ⁡ - ψ *

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

São conhecidas duas componentes da velocidade de um campo de escoamento em regime permanente, incompressível: u =a x +b x y + c y 2 e v = a x z - b y z 2 onde a ,b ,ec são constantes. Está faltando a
A componente de velocidade u de um campo de escoamento permanente, bidimensional, incompressível é u =a x 2 -b x y , onde a e b são constantes. A componente de velocidade v é desconhecida. Encontre um
Um bloco desliza para baixo em uma parede longa, reta, inclinada, com a velocidade V , sobre um filme fino de óleo de espessura h (Figura P9-113).O peso do bloco é W ,e sua área de contato com a filme
Considere o seguinte escoamento incompressível bidimensional, que claramente satisfaz a continuidade: u = U 0 = c o n s t a n t e ,v = V 0 = c o n s t a n t e Encontre a função corrente ψ ( r , θ ) pa
Considere o potencial de velocidade incompressível bidimensional ϕ = x y + x 2 - y 2 . (a) É verdade que ∇ 2 ϕ = 0 , e, em caso afirmativo, o que isso significa? (b) Se ela existe, encontre a função c