Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 115
A boia de mastro de 50 mm por 50 mm por 3,65 m da Figura P2.113 tem 2,3 kg de aço na extremidade e se apoia sobre uma pedra, como mostra a Figura P2.115. Calcule o ângulo theta no qual a boia se equilibrará, considerando que a pedra não exerce nenhum momento sobre o mastro.
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
A primeira ideia que a gente tem que ter da questão é de qual assunto ela faz parte. Esse problema em específico é referente à seção 2.8 do livro, chamada “Empuxo; princípios de Arquimedes”.
Nesse problema, temos uma boia de mastro de base e com comprimento de e densidade . Um peso de de aço está apoiado na extremidade e está apoiado em uma pedra, como demonstra a figura que ilustra a questão.
Como vocês podem ver pela ilustração, existe um ângulo do mastro com relação ao plano vertical. A questão quer que a gente calcule esse ângulo .
Pra isso, devemos entender que temos duas forças atuando aqui: a força peso do corpo e o empuxo exercido pela água na boia .
Para calcular o peso, podemos utilizar a equação:
Sendo: o peso específico da água e o volume da boia.
Para calcular o empuxo, fazemos:
Sendo e o volume da boia submersa.
Nos próximos passos, vamos utilizar essas forças em um balanço de momento para calcular o ângulo .
Vem comigo pra resolver a questão!
Passo 2
Pra começo de conversa, vamos olhar esse esquema abaixo antes da gente começar com esse passo:
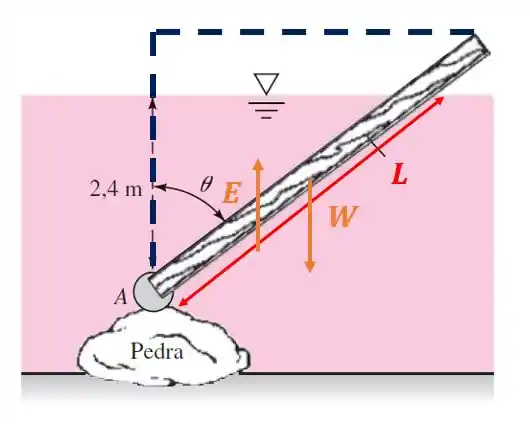
Vamos chamar de o comprimento da boia que está submerso. Sim, como você pode perceber pela imagem, não temos o valor desse comprimento. Vamos ter que descobri-lo a partir de um balanço de momento.
Mas primeiro, vamos calcular o peso da boia:
Para o empuxo, iremos achar uma expressão dependente de a partir da equação que eu te mostrei no Passo 1:
Como eu disse pra vocês no Passo 1, iremos fazer um balanço de momento no próximo passo para calcular o valor de e a partir dele calcular o ângulo . Pra isso, devemos calcular as linhas de ação das forças até o ponto .
Como você pode ver pela figura, podemos calcular as linhas de aplicação a partir a partir de relações trigonométricas.
Supomos então que a boia é uniforme. Portanto, podemos considerar que todo o peso e o Empuxo estão concentrados em um ponto: no caso do peso, no meio da boia, e do empuxo, no meio da parte submersa.
Dessa forma, podemos definir a distância de aplicação da força peso com relação ao fio será e a distância de aplicação do empuxo será .
Passo 3
Pra finalizar a questão, vamo fazer um balanço de momento das forças peso e empuxo com relação ao ponto .
Como queremos que a boia esteja equilibrada, isso significa dizer que o somatório de momento das forças aplicadas nela é zero. Ou seja, nosso balanço de momentos é:
Sendo: e as linhas de aplicação com relação a do peso e do empuxo, que já calculamos no passo anterior.
Substituindo os valores na equação, teremos:
Agora, podemos calcular o ângulo . Devemos voltar pra figura que eu te mostrei no passo anterior.
Pela figura, sabemos que a distância vertical até a superfície livre é de . Logo, basta fazermos uma simples relação trigonométrica:
Pronto, matamos a questão juntos!
Resposta
O ângulo no qual a boia se equilibrará é