Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 99
Balões científicos operando em uma pressão de equilíbrio com o ambiente têm sido usados para levar instrumentos a altitudes extremamente elevadas. Um desses balões, construído em poliéster com espessura de 0,013 mm e diâmetro de 120 m, elevou uma carga de 230 kg. A densidade relativa do material do balão é 1,28. Determine a altitude na qual o hélio usado no balão está em equilíbrio térmico com o ar ambiente. Suponha que o balão seja perfeitamente esférico.
Passo 1
O problema que vamos resolver é sobre um balão esférico cheio de hélio que levanta uma carga útil de massa . Na altitude, o hélio e o ar estavam em equilíbrio térmico. O diâmetro do balão é e a gravidade específica do material da pele é de . Tendo isso, devemos encontrar a altitude em que o balão subiu.
Aplicaremos as equações hidrostáticas neste sistema:
(a força de empuxo é igual à massa do fluido deslocado)
(Equação de estado ideal dos gases)
Para o problema, consideramos: fluido estático e incompressível; equilíbrio estático a de altitude; e comportamento ideal do gás.
Passo 2
Temos o seguinte diagrama de corpo livre:
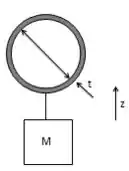
Substituindo a força flutuante e sabendo que a massa é densidade vezes o volume:
Calculamos o volume do balão e o volume do material:
Substituindo na equação, temos:
A partir da equação de estado ideal dos gases e lembrando que a pressão e a temperatura do ar e hélio são iguais:
Substituindo valores conhecidos, usando a tabela do Apêndice A que contem no final do:
Para determinar a altitude, precisamos verificar essa relação com os dados da Tabela A.3. Para a relação pressão/temperatura achamos:
Prontinho!!