Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 34
Um motor de foguete opera em regime permanente como mostra a figura abaixo. Os produtos da combustão que escoam através do bocal de descarga aproximam-se de um gás perfeito com peso molecular de 28. Para as condições dadas, calcule em m/s.
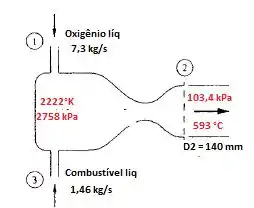
Passo 1
Aqui é uma misturinha de termodinâmica com mecânica dos fluidos haha
Na saída a gente tem que a densidade do fluido será dada pela equação abaixo, lembrando que R deve ser dado por 8313/MM.
Passo 2
Pela conservação da massa, a gente tem que a vazão de saída deve ser igual a vazão de entrada de combustível e oxigênio, ou seja, .
Resolvendo para V2, temos que:
Resposta
Exercícios de Livros Relacionados
Na Figura FE3.1, água sai de um bocal à pressão atmosférica de 101 kPa. Se a vazão volumétrica é de 606 L/min, qual é a velocidade média na seção 1?(a) 2,6 m/s, (b) 0,81 m/s, (c) 93 m/s, (d) 23 m/s, (
Um tanque rígido de volume v = 1,0m 3 é enchido inicialmente com ar a 20°C e p 0 = 100k P a . No tempo t = 0 , uma bomba de vácuo é ligada e evacua ar a uma vazão volumétrica constante, Q = 80L / m i
Um engenheiro afirma que o escoamento de óleo SAE 30W a 20°C, por um tubo liso de 5cm de diâmetro a 1 milhão de N/h, é laminar. Você concorda? Um milhão de newtons é muito, de modo que isso soa como u
Para o escoamento de óleo SAE 30 por um tubo de 5 cm de diâmetro, Fig. A.1, para qual vazão em m3/h devemos esperar transição para a turbulência a (a) 20 °C e (b) 100°C?
Ar a aproximadamente 1 atm escoa por um tubo horizontal de 4 cm de diâmetro. (a) Deduza uma fórmula para Qmáx, a vazão volumétrica máxima para a qual o escoamento permanece laminar, e plote Qmáx em fu