Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 97
Bolhas de hidrogênio são usadas para a visualização de linhas de emissão no filme Flow Visualization. O diâmetro típico de uma bolha de hidrogênio é . As bolhas tendem a subir lentamente na água por causa do empuxo; eventualmente, elas atingem
uma velocidade terminal em relação à água. A força de arrasto da água sobre a bolha é dada por , em que é a viscosidade da água eé a velocidade da bolha relativa à água. Determine a força de empuxo que atua sobre uma bolha de hidrogênio imersa na água. Estime a velocidade terminal de uma bolha em ascensão na água.
Passo 1
Para esse problema, temos bolhas de hidrogênio, precisamos encontrar a força de flutuabilidade na bolha e a velocidade terminal na água. Para isso, utilizaremos as seguintes equações:
, força de empuxo
, somatório de forças no sentido de
Pelo diagrama podemos fazer a seguinte analise de forças:
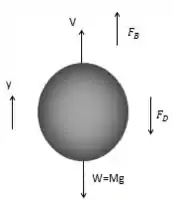
Calculando a força de empuxo ou :
Passo 2
Para a velocidade terminal, temos:
onde ignoramos , o peso da bolha, por quase não fazer diferença.
Consequentemente,
Pela tabela A.7 do livro, encontramos a viscosidade dinâmica , logo:
Portanto, ocorre o que o professor Kline no filme "Visualização de Fluxo" afirma: as bolhas aumentam lentamente!
Resposta
e .