Determine o peso específico da esfera mostrada na figura, se o seu volume é de . Enuncie todas as considerações feitas. Qual será a posição de equilíbrio da esfera, se o peso for removido?
Passo 1
Temos nesse problema alguns dados sobre a esfera e seu peso. Vamos determinar o da esfera e a posição de equilíbrio quando flutuando livremente.
Usaremos as seguintes equações:
Consideramos a massa como .
Passo 2
Começamos pela analise do diagrama:
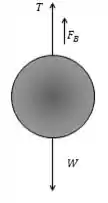
Onde: , e .
Substituindo,
Logo,
Portanto, o peso específico é:
Logo,
Passo 3
Agora, para o equilíbrio ao flutuar, repetimos o balanço de força com :
Com . O volume parcial da esfera pode ser dado por:
onde é profundidade submersa e é o raio da esfera.
Assim, calculando o raio temos:
Então, substituindo no peso:
Usando uma calculadora avançada, temos que .