Uma bomba centrífuga de 37 cm de diâmetro, operando a 2.140 rpm com água a 20 °C, produz os seguintes dados de desempenho:
(a) Determine o ponto de máximo rendimento. (b) Faça um gráfico de CH em função de CQ. (c) Se quisermos usar essa mesma família de bombas para bombear 442 l/s de querosene a 20 °C com uma potência de eixo de 400 kW, qual é a rotação da bomba (em rpm) e o tamanho do rotor (em cm) necessários? Qual a altura de carga que será desenvolvida?
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
Nessa questão, temos uma bomba centrífuga com diâmetro operando uma rotação de , bombeando água a ().O problema nos mostra também uma tabela com os dados de desempenho pra essa bomba.
O enunciado nos pede então pra determinar o ponto de máximo rendimento, fazer um gráfico do coeficiente de altura de carga em função de e, por fim, pra gente calcular as propriedades ao usar essa mesma família de bombas pra bombear querosene ( a uma vazão de e potência de eixo .
Vem comigo pra gente matar esse problema juntos!

Passo 2
Pra começar a questão, vamos resolver a letra (a) e determinar o ponto de máximo rendimento.
Primeiro, devemos usar a tabela fornecida pelo enunciado pra calcular os rendimentos pra cada uma das vazões, utilizando a Equação 11.5:
Realizando os cálculos pra cada um dos pontos a gente fica com a seguinte tabela:

Como a gente consegue ver na tabela acima, o maior valor de rendimento é no ponto onde a vazão volumétrica é .
Passo 3
Agora, vamos resolver a letra (b) e fazer um gráfico de em função de .
Pra isso, vamos utilizar as Equações 11.23 (página 777):
Calculando os coeficientes pra cada um dos pontos, vamos obter a seguinte tabela:

Com a tabela pronta, podemos plotar o gráfico de em função de :
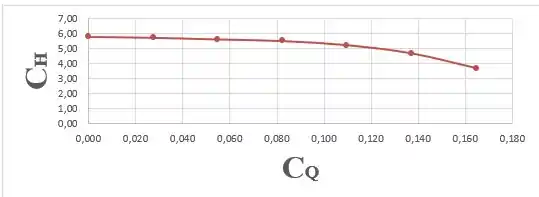
Passo 4
Pra finalizar a questão, vamo resolver a letra (c).
Em primeiro lugar, vamos calcular os coeficientes adimensionais no ponto de projeto. Do passo anterior, sabemos que nesse ponto e . Jpa pde ser calculado como:
Com esses coeficientes adimensionais no ponto de projeto, podemos usar as leis de semelhança pra calcular a rotação , o diâmetro e altura de carga no ponto de projeto pra bombear querosene a , e .
Sendo assim, vamos obter o seguinte sistema de equações:
Resolvendo pra e :
Da mesma forma, podemos calcular a nova carga usando e :
Pronto, matamos a questão juntos!

Resposta
(a) O maior valor de rendimento é no ponto onde a vazão volumétrica é .
(b) O gráfico se encontra no Passo 3
(c) , e