Uma bomba manual de bicicleta pode ser usada como um atomizador para gerar uma nevoa fina de tinta ou pesticida forçando o ar a uma alta velocidade através de um pequeno
orifício e colocando um tubo curto entre o reservatório de liquido e o jato de ar a alta velocidade cuja baixa pressão move o liquido para cima através do tubo. Em tal atomizador, o metro do orifício é de , a distância vertical entre o nível do liquido do tubo e o orifício é de , e a perfuração (diâmetro) e o movimento da bomba de ar são de e , respectivamente. Se as condições atmosféricas são de a , determine a velocidade mínima com a qual o pistão deve se mover no cilindro durante o bombeamento para iniciar
o efeito de atomização. O reservatório de liquido é aberto para a atmosfera.
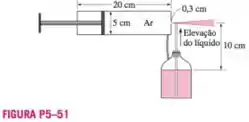
Passo 1
Bom, nesse problema temos uma bomba manual liberando ar e devemos determinar a velocidade mínima para que o pistão se mova no cilindro durante o bombeamento a fim de iniciar o efeito de atomização.
Começamos montando o diagrama do problema, estabelecendo os pontos:
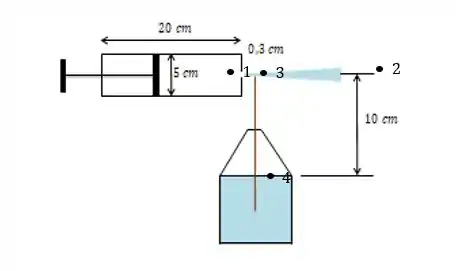
Como as perdas por atrito são desprezíveis, podemos usar a equação de Bernoulli para o ar, nos pontos e e para a água nos pontose , beleza?!
Passo 2
Vamos considerar , e por fim .
Agora vamos escrever Bernoulli para os pontos e :
Sabendo que e , temos:
Organizando:
Temos as referências para calcular a densidade do ar, para essa pressão e temperatura a constante do ar é :
Agora para a água:
Se então , lembrando que as velocidades podem ser aproximadas para zero, e a :
Arrumando a casa:
Substituindo na equação anterior, ficamos com:
Passo 3
Já podemos calcular :
Substituindo:
Passo 4
A nossa resposta ainda não esta completa, pois se pensarmos mais um pouco, quando o ar sai do pistão, linhas de fluxo de ar se curvam ao redor da parte superior do tubo. Ou seja:
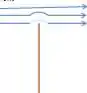
Se olharmos bem do instante em que esta no pistão para a saída, é como se tivéssemos um tubo de Venturi (assunto para próximos capítulos).
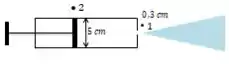
Mas basicamente temos:
Simplificando e isolando :
Substituindo os dados:
Prontinho!!