Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 11.Problemas - Ex. 70

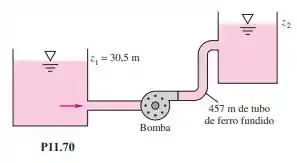
A bomba do Problema P11.28, operando a 2.134   r p m , é usada para fornecer água a 20 ° C para o sistema da Figura P11.70. (a) Se ela estiver operando no PMR, qual será a elevação z 2 adequada? (b) Se z 2 = 68,6   m e d = 203   m m , qual é a vazão?

Passo 1

E ai, pronto para resolver essa questão comigo?

Então, fica de olho!

Começamos o nosso problema expondo os dados do Problema P11.28 na tabela a seguir:

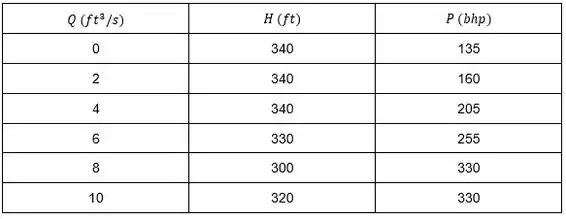
Escrevendo a relação de eficiência:

n = γ Q H P

Substituindo os valores de descarga, carga e potência de entrada, o ponto de melhor eficiência está em:

Q = 6   f t 3 / s

H = 330   f t

Passo 2

Letra a)

Escrevendo a relação para altura de carga total:

H = z 2 - z 1 + f L V 2 2 g d

Da equação de continuidade:

Q = π 4 d 2 V

Isolando V :

V = Q π D d 2

Substituindo Q = 6   f t 3 / s e d = 8   i n :

v = 6 π 4 ⋅ 8   i n ⋅ 1   f t 12   i n 2

v = 17,2   f t / s

Calculando o número de Reynolds:

R e = ρ V d μ

Substituindo os dados:

R e = 1,94 ⋅ 17,2 ⋅ 8   i n ⋅ 1   f t 12   i n 2,09 × 10 - 5

R e = 1,06 × 10 6

A relação de rugosidade relativa do tubo é dada por:

ε d = 0,00085 8   i n ⋅ 1   f t 12   i n = 0,00128

A partir do Diagrama de Moody, temos:

f = 0,0211

Substituindo os dados na equação que expomos no começo deste passo:

330 = z 2 - 100 + 0,0211 ⋅ 1500 ⋅ 17,2 2 ⋅ 32,2 ⋅ 8   i n ⋅ 1   f t 12   i n

z 2 = 212   f t

Portanto, a elevação do reservatório 2, quando a bomba está operando no BEP é de 212   f t .

Passo 3

Letra b)

Escrevendo a relação para a altura de carga total no sistema, quando o z 2 for alterado para  68,6   m   ( 225   f t ) e elevação d = 203   m m   ( 8   i n ) :

H = z 2 - z 1 + f L V 2 2 g d

Substituindo os dados:

H = 225 - 100 + f ⋅ 1500 ⋅ V 2 2 ⋅ 32,2 ⋅ 8   i n ⋅ 1   f t 12   i n

H = 125 + f ⋅ 1500 ⋅ V 2 42,93

Da equação de continuidade:

Q = π 4 d 2 V

Isolando V :

V = Q π D d 2

Substituindo os dados:

V = Q π 4 ⋅ 8   i n ⋅ 1   f t 12   i n 2

V = 2,865 ⋅ Q

Substituindo V na nossa equação e tendo f = 0,0211 :

H = 125 + f ⋅ 1500 42,93 ⋅ 2,865 ⋅ Q 2

H = 125 + 0,0211 ⋅ ( 286,8 ⋅ Q 2 )

Com H = 330   f t , temos que Q é igual a:

330 = 125 + 0,0211 ⋅ 286,8 ⋅ Q 2

Q = 5,8   f t 3 / s

Para z 2 = 68,6   m   ( 225   f t ) teremos uma vazão de 5,8   f t 3 / s .

E assim a gente termina a nossa questão!

Te espero na próxima!

Resposta

a )   z 2 = 212   f t

b )   Q = 5,8   f t 3 / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

14-75 Verifique se a velocidade específica da turbina e da bomba estão relacionadas da seguinte maneira: N s t = N s p η t u r b i n a .
Calcule a velocidade específica da bomba do Exemplo 14-11 ao seu ponto de melhor eficiência. Forneça respostas nas formas adimensionais e em unidades comuns nos EUA. Qual é o tipo dessa bomba?
14-79 Calcule a velocidade específica da turbina hidráulica de Smith Mountain da Figura 14-90. Ela se classifica dentro do intervalo de de N S t apropriado para aquele tipo de turbina?
14-74 Considere a bomba do Problema 14-73. Suponhamos que a bomba seja modificada pela inclusão de ura motor diferente, cuja rpm é metade daquela da bomba original. Se as bombasoperarem a pontos homól
14-76 Considere uma bomba-turbina que opera tanto como bomba quanto como turbina. Sob condições nas quais a velocidade rotacional ω e a vazão V ˙ são iguais para a bomba e a turbina, verifique se as v