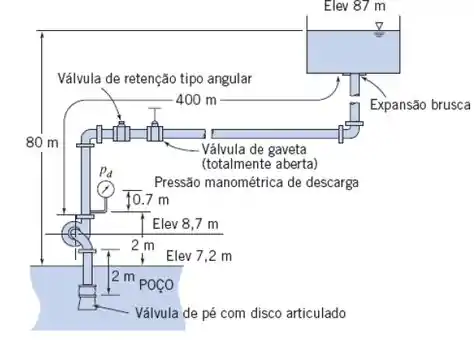
Uma bomba, no sistema mostrado, retira água de um poço e lança-a em um tanque aberto através de 400 m de tubo novo de aço com diâmetro nominal de 10 cm. O tubo vertical da aspiração (sucção) tem comprimento de 2 m e inclui uma válvula de pé com disco articulado e um cotovelo de 90°. A linha de recalque (descarga) inclui dois cotovelos padronizados, de 90°, uma válvula angular de retenção e uma válvula de gaveta totalmente aberta. A vazão de projeto é 800 L/min. Determine as perdas de carga nas linhas de sucção e de descarga. Calcule o NPSHA. Selecione uma bomba adequada para esta aplicação.

Agora com essa velocidade, conseguimos encontrar o número de Reynolds, para isso, vamos pegar alguns dados da Tabela A.7 do livro, inclusive uns que usaremos mais tarde:

Então, Reynolds será:

Agora, para encontrar o fator de atrito, precisamos primeiro pegar o dado referente à rugosidade da tubulação, que se encontra na tabela a seguir presente no capítulo 8:

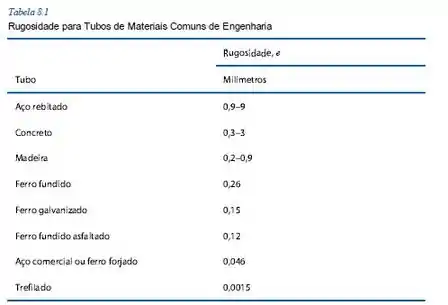
Então, como temos aço comercial, teremos . Então agora podemos usar a equação de Colebrook e descobrir o valor do fator de atrito:

Substituindo os valores conhecidos (lembrando que só conseguimos resolver essa equação com o auxílio de uma calculadora), temos:

Agora vamos voltar à equação do equilíbrio de energia do passo 1:

E substituir a expressão encontrada para a perda de carga específica no passo 1:

Agora precisamos recorrer às tabelas 8.2 e 8.4 apresentadas no livro para encontrar os coeficientes de perda:

Dessa forma, como temos uma entrada reentrante, teremos:

E, como temos uma válvula de pé com disco articulado teremos um comprimento equivalente:

Então, agora, substituindo todos os valores conhecidos na equação de energia, temos:

Então, a pressão manométrica em 2 será:

E os termos de perda de carga correspondem a:

Agora, para encontrar o NPSHA, basta fazer:

Substituindo os valores conhecidos, temos:

Para selecionar uma bomba para o sistema, precisamos da vazão utilizada e da altura de carga, já temos a vazão, só nos resta calcular a altura de carga, podemos fazer isso aplicando a equação de energia utilizada no passo 1, só que agora entre o primeiro reservatório (ponto 1) e o segundo (ponto 2), então, temos:

Nesse caso temos , então os termos de pressão se cancelam, sabemos também que podemos considerar as velocidades nos reservatórios iguais a zero, então , e a equação se torna:

Substituindo a expressão para a perda de carga encontrada no passo 1, temos:

Só que agora estamos contemplando o sistema completo, então temos:

E, para o comprimento equivalente, devemos reccorer à tabela do passo 3, como temos uma válvula de disco articulado, uma válvula de retenção angular, uma válvula de gaveta e dois cotovelos padrão de 90°, o comprimento equivalente será:

E, agora para as perdas localizadas, já sabemos que temos uma entrada reentrante no reservatório 1, mas temos também uma expansão brusca no reservatório 2, para a expansão brusca, temos o seguinte diagrama:

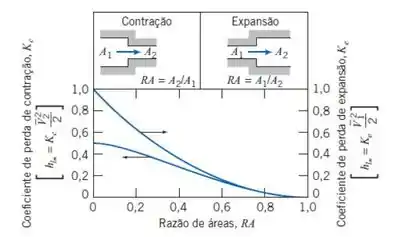
Então, para a expansão brusca teremos , dessa forma, será:

Agora que temos todos os dados, podemos substituir os valores conhecidos na equação de energia do passo 5, então:

No entanto essa é a carga específica, para obter a carga em metros, devemos dividir esse valor por , então:

Para essa altura de carga e para a vazão , com o diagrama de seleção de bombas a seguir, temos:

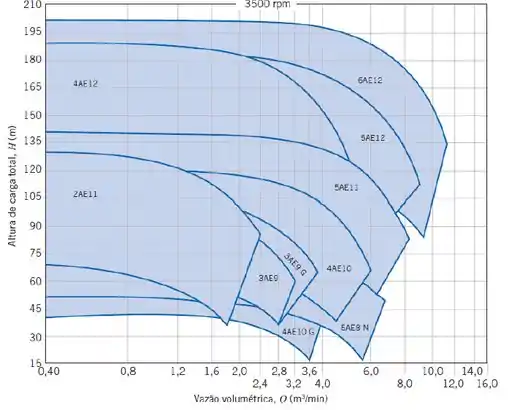
Então, podemos escolher uma bomba 2AE11 para atender ao projeto