Na bomba de água do Problema 10.8, a carcaça da bomba age como um difusor que converte da altura de carga da velocidade absoluta na saída do rotor em aumento de pressão estática. A perda de carga através dos canais de admissão e de descarga do rotor é vez a altura de carga da componente radial da velocidade na saída do rotor. Estime a vazão volumétrica, o aumento de altura de carga, a potência de entrada e a eficiência da bomba no ponto de máxima eficiência. Considere que o torque para superar perdas existentes de mancal, selo e giro (spin) seja do torque ideal para .

Encontrando a velocidade angular :

Sendo a velocidade de :

Agora, calcularemos a velocidade horizontal de saída :

Substituindo os dados:

Calculando :

Substituindo os dados conhecidos:

Calculando :

Substituindo os valores conhecidos:

Assim, conseguimos obter a velocidade absoluta de saída:

Calculando o aumento teórico de altura:

Sendo e , temos:

Sabendo que a carcaça da bomba age como um difusor que converte da altura de carga da velocidade absoluta na saída do rotor em aumento de pressão estática. A perda de carga através dos canais de admissão e de descarga do rotor é vez a altura de carga da componente radial da velocidade na saída do rotor.

Calcularemos a elevação de altura real:

Substituindo os dados:

Considerando que o torque para superar perdas existentes de mancal, selo e giro (spin) seja do torque ideal para .

Calculando o torque necessário:

Substituindo os dados e sabendo que :

A eficiência da bomba é dada pela razão da potência de saída pela de entrada:

Substituindo os dados:

Repetiremos os cálculos para diferentes vazões para obtermos o ponto máximo de eficiência:

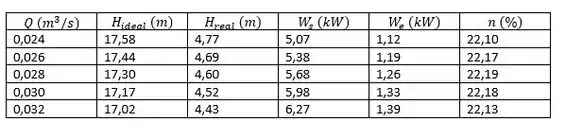
Percebemos que o ponto máximo de eficiência se dá quando .