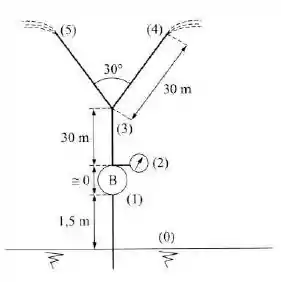
Uma bomba succiona água de um reservatório, cujo nível se encontra a da sua seção de entrada, por um tubo de diâmetro de . Na saída da bomba encontra-se um manômetro metálico que indica uma pressão de . A tubulação de recalque tem diâmetro de por um comprimento de e nesse ponto ela se bifurca em dois ramais simétricos de de diâmetro e de comprimento, que formam um ângulo de entre si.

Dados:

• Perda de carga nas tubulações de de diâmetro: por metro de tubulação;
• Perda de carga nas tubulações de de diâmetro: por metro de tubulação.

Determinar:

1. A vazão em volume em ;
2. A altura ou carga manométrica da bomba.

A perda de carga para cada tubulação é dada por:

Temos também que:

E:

Para calcular a vazão volumétrica, podemos aplicar Bernoulli entre :

Como a área de e é a mesma, temos que:

Agora vamos estudar como se dá a bifurcação do escoamento em :

Portanto:

Conhecendo as quantidades relacionadas ao ponto , podemos estudar o fluxo de energia na bifurcação, sabendo que:

Assumindo que a saída em e em estão à pressão atmosférica e substituindo a relação de velocidades encontrada, temos que:

A vazão será:

Para calcular a carga manométrica da bomba, vamos aplicar Bernoulli entre os pontos . Supondo que o fluido em esteja em um tanque de grandes dimensões à pressão atmosférica: