Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo Exercícios Selecionados.- - Ex. 20

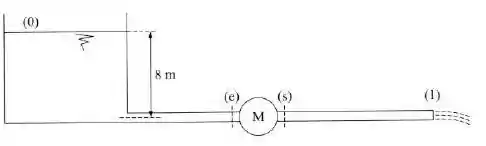
Na instalação da figura, a potência trocada entre o fluido e a máquina é 7,14   k W . Se o escoamento é perfeitamente isotérmico e o fluxo de calor dissipado entre 0 e e é 4,2   k W , determinar:

  1. O tipo de máquina;
  2. O fluxo de calor entre s e 1 em k W .

Dados: γ H 2 O = 10 4 N / m 3 ; Q = 42   L / s ; g = 10   m / s 2 ; A = 105   c m 2 (área da seção da tubulação).

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Para descobrir o tipo de máquina precisamos saber se ela adiciona ou retira carga manométrica do escoamento. Caso adicione ela será uma bomba, caso retire será uma turbina.

A velocidade do escoamento é dada por:

v e = Q e A e = 42 ⋅ 10 - 3 105 ⋅ 10 - 4

v e = 4   m / s

Agora vamos utilizar Bernoulli no trecho 0 - e para encontrar a pressão de escoamento:

P 0 γ + v 0 2 2 g + z 0 = P e γ + v e 2 2 g + z e + N 0 , e γ Q e

Substituindo os valores conhecidos, temos que:

8 = P e 10 4 + 4 2 2 0 + 4200 10 4 ⋅ 42 ⋅ 10 - 3

P e = - 28   k P a

Como o escoamento flui dos pontos de maior pressão para os pontos de menor pressão. Podemos garantir que a máquina fornece potência ao escoamento, tratando-se de uma bomba.

Passo 2

Para calcular a energia dissipada no trecho s - 1 , podemos utilizar conservação de energia:

E 0 + E B + E 1 + E p 0 , e + E p s , 1

γ Q P 0 γ + v 0 2 2 g + z 0 + E B = γ Q P 1 γ + v 1 2 2 g + z 1 + E p 0 , e + E p s , 1

Fazendo as devidas considerações para o sistema, teremos que:

γ Q z 0 + E B = γ Q v 1 2 2 g + E p 0 , e + E p s , 1

10 4 ⋅ 42 ⋅ 10 - 3 ⋅ 8 + 7,14 ⋅ 10 3 = 10 4 ⋅ 42 ⋅ 10 - 3 ⋅ 4 2 20 + 4,2 ⋅ 10 3 + E p s , 1

E p s , 1 = 6   k W

Resposta

a )   Bomba

b )   E p s , 1 = 6   k W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabe-se que estão presentes condições plenamente desenvolvidas no escoamento de água, com vazão de 0,01k g / s e a 27°C, em um tubo com 25 mm de diâmetro. Qual é a velocidade máxima da água no tubo? Q
Qual é a queda de pressão associada ao escoamento de água a 27ºC e a uma velocidade média de 0,2 m s através de um tubo de ferro fundido, com 600 m de comprimento e diâmetro interno de 0,15 m?
Os perfis de velocidades e de temperaturas para o escoamento laminar em um tubo com raio r 0=10m m têm as formas: u r = 0,11 - r r 0 2 T r = 344,8 + 75,0 r r 0 2 - 18,8 r r 0 4 Com unidades de m/s e K
Água a 27°C escoa, com uma velocidade média de 1 m s , através de uma tubulação com 1 km de comprimento e 0,25 m de diâmetro interno. Determine a queda de pressão ao longo do comprimento da tubulação
No Capítulo 1 foi afirmado que, para líquidos incompressíveis, o trabalho de escoamento pode normalmente ser desprezado na equação da energia para escoamentos em regime estacionário (Equação 1.12d). N