Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 65
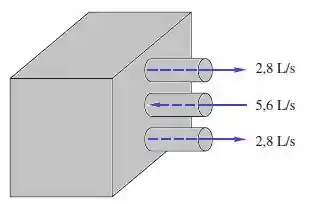
A caixa abaixo tem três orifícios de 12,5 mm do lado direito. As vazões de água a 20°C indicadas são permanentes, mas os detalhes do interior são desconhecidos. Calcule a força, se houver, que esse escoamento de água exerce sobre a caixa.
Passo 1
Bem, primeiramente o que vamos fazer é calcular as velocidades que saem de cada orifício, beleza?
E vamos inicialmente transformar para uma unidade que gostamos de trabalhar, que é m³/s
Passo 2
Vamos agora fazer o balanço de forças no eixo x no nosso volume de controle em torno da caixa.
Onde e
Passo 3
Agora precisamos lembrar também que
Resposta
Exercícios de Livros Relacionados
Como se pode observar frequentemente em uma pia de cozinha quando a torneira está aberta, um escoamento com alta velocidade em um canal ( V 1 , h 1 ) pode “saltar” para uma condição de baixa velocidad
A bomba centrífuga da Figura P3.116 tem um escoamento com vazão Q, saindo do rotor com um ângulo θ 2 , relativo às pás, como mostra a figura. O fluido entra axialmente na seção 1. Considerando escoame
Um trenó de Massa M, movido a foguete, Figura P3.108, deve ser desacelerado por uma concha de largura b normal ao papel e imersa na água à profundidade h, criando um jato de 60° para cima. O empuxo do
Admita que o foguete da Figura E3.12 inicie o movimento em z = 0 , com velocidade de saída e vazão em massa de saída constantes, e suba verticalmente com força de arrasto zero. (a) Mostre que, enquant
Um líquido de massa especifica ρ escoa em uma curva a 90 ° , como mostra a Figura P3.125, e sai verticalmente e uniformemente por um trecho poroso de comprimento L. Desprezando os pesos do tubo e do l