Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 102
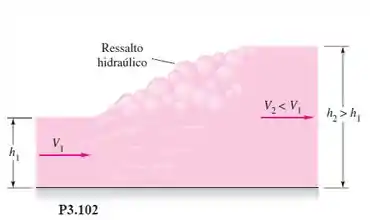
Como se pode observar frequentemente em uma pia de cozinha quando a torneira está aberta, um escoamento com alta velocidade em um canal pode “saltar” para uma condição de baixa velocidade e baixa energia , como na Figura P3.102. As pressões nas seções 1 e 2 são aproximadamente hidrostáticas e o atrito na parede é desprezível. Use as relações de continuidade e quantidade de movimento para encontrar e em termos de (.
Passo 1
Bora pra mais uma!
Vamo começar fazendo uma relação de continuidade, temos:
Isolando :
Passo 2
Partindo então para uma relação de quantidade de movimento, teremos, num movimento em x:
Teremos que, ao rearranjar a equação para encontrar uma relação para :
Resposta
Exercícios de Livros Relacionados
Um pequeno motor de foguete, a combustível sólido, é testado em uma bancada. A câmara de combustão é circular, com 100m m de diâmetro. O combustível, de massa específica 1660k g / m 3 , queima uniform
Considere a configuração do jato vertical atingindo o disco vertical conforme mostrado no Problema 4.158 . Suponha que o disco seja largado do repouso a uma altura inicial de 2m acima do plano de saíd
Um pequeno motor de foguete é utilizado para acionar um dispositivo a “jato portátil” destinado a elevar um só astronauta acima da superfície da Lua. O motor do foguete produz um jato uniforme com vel
O tanque móvel mostrado deve ser desacelerado pelo abaixamento de uma concha que capta água de um reservatório. A massa e a velocidade iniciais do tanque, com seu conteúdo, são m 0 e u 0 , respectivam
Deseja-se uma bomba que, acoplada a um motor de 3450 rpm, produza uma altura manométrica teórica de 80 m. O ângulo de entrada das pás deve ser de 15º e o de saída, de 30º. Sendo d 1 = 10c m , quanto d