Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 2.Exercício - Ex. 21

Calcular a pressão na câmara ( 1 ) sabendo que o pistão se desloca com uma velocidade constante de 1,2   m / s e a indicação do manômetro metálico é 10   k P a . Dados: D = 1   m ;   L = 0,2   m ;   v ó l e o = 10 - 3 m 2 / s ;   D p = 0,998   m ;   γ ó l e o = 8.000   N / m 3 ;   g = 10   m 2 s . Observação: considerar o nível do óleo constante.

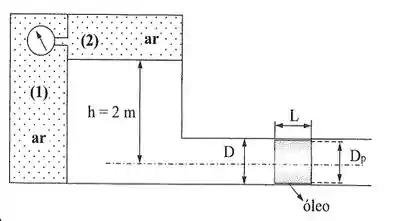
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Observe a seguinte situação:

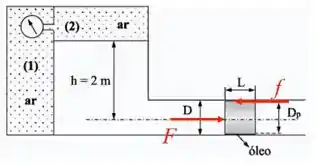
Esse desenho nos mostra o que está acontecendo no nosso sistema.

Existe a força F causada pela pressão P que é a pressão da coluna de óleo mais a pressão em 2 . Temos também a força de cisalhamento f causada pelo atrito do óleo com a parede. Essas forças devem ser equivalentes para que o sistema esteja em equilíbrio. Logo:

F = f

Como a força causada pela pressão é dada por:

F = P ⋅ A

Onde A é a área da seção transversal e vale:

A = π D p 2 4

E a força de cisalhamento é dada por:

f = τ ⋅ A l

Onde A l é a área da seção lateral e vale:

A l = π D p L

E:

τ = μ v ε

Temos que:

P ⋅ A = τ ⋅ A l

P ⋅ π D p 2 4 = μ v ε ⋅ π D p L

Passo 2

Agora que temos uma expressão para descobrir a pressão, é só substituir os valores:

P ⋅ π D p 2 4 = μ v ε ⋅ π D p L

P = 4 μ v L ε D p

Seja:

μ = v γ g = 10 - 3 8000 10

μ = 0,8

E:

ε = D - D p 2

ε = 1 - 0,998 2

ε = 0,001   m

Temos que:

P = 4 ( 0,8 ) ( 1,2 ) ( 0,2 ) ( 0,001 ) ( 0,998 )

P = 769,5   P a

Passo 3

Mas qual o motivo de termos encontrado esta pressão? Veja bem... A pressão manométrica é dada pela pressão interna menos a externa. No caso seria:

P m = P 2 - P 1

Então precisamos saber a pressão em 2 para descobrir a pressão em 1 .

E a pressão no cilindro, que é a que encontramos, é dada pela soma da pressão em 2 com a pressão da coluna de óleo:

P = P 2 + γ h

Logo:

P 2 = P - γ h

P 2 = 769,5 - 8000 2

P 2 = - 15230,5

Logo:

P 1 = P 2 - P m

P 1 = - 15230,5 - 10000

P 1 = - 25230,5   P a

A pressão em 1 será:

P 1 = - 25,23   k P a

Resposta

P 1 = - 25,23   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

The Hoover Dam, in Arizona, encloses Lake Mead,which contains 10 trillion gallons of water. The dam is1200 ft wide and the lake is 500 ft deep. (a) Estimate thehydrostatic force on the dam, in MN. (b)
For the three-liquid system shown, compute h1 and h2.Neglect the air density
Suppose, which is possible, that there is a half-miledeep lake of pure ethanol on the surface of Mars. Estimate the absolute pressure, in Pa, at the bottom of thisspeculative lake.
Quito, Ecuador, has an average altitude of 9350 ft. On a standard day, pressure gage A in a laboratory experiment reads63 kPa and gage B reads 105 kPa. Express these readings ingage pressure or vacuum
Pressure gages, such as the bourdon gage in Fig. P2.4, arecalibrated with a deadweight piston. If the bourdon gageis designed to rotate the pointer 10 degrees for every2 psig of internal pressure, how