Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 11.Problemas - Ex. 62
Calcule a profundidade crítica para o canal no Problema 11.41. (Correção: o enunciado na verdade se refere ao Problema 11.42, o 11.41 não é um canal e nem faz parte dos problemas de escoamento uniforme).
Passo 1
Beleza! Sabemos que a equação da descarga para o sistema é dada por:
E que a equação da profundidade crítica para um canal retangular é:
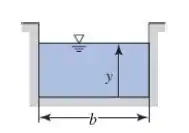
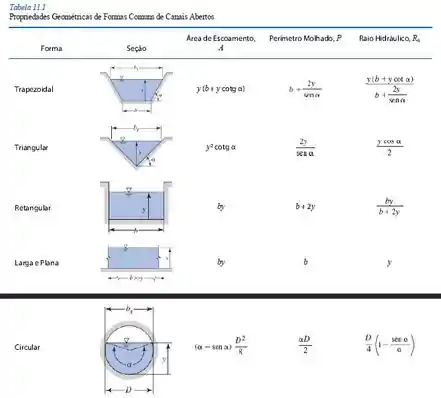
Com o auxílio da tabela de geometria fornecida nessa seção, temos:
Passo 2
Substituindo os valores conhecidos nas equações para e , temos:
Passo 3
Então, substituindo os valores conhecidos na equação de descarga, temos:
Agora, substituindo os valores conhecidos na equação para a profundidade crítica, temos:
Resposta
Exercícios de Livros Relacionados
Considere um canal retangular de 3 m de largura sobre um declive de 1°. Se a profundidade da água é de 2 m, o raio hidráulico é:(a) 0,43 m, (b) 0,6 m, (c) 0,86 m, (d) 1,0 m, (e) 1,2 m
Em fevereiro de 1998, houve o rompimento da barragem de terra da represa California Jim, no sul de Rhode Island. A enchente resultante provocou uma destruição temporária no povoado de Peace Dale, próx
Um tubo de drenagem circular, de concreto sem acabamento, é assentado em um declive de 0,0025 e está planejado para conduzir de 1,4 a 8,5 m3/s de água drenada. As restrições do projeto são que (1) a p
Estenda o Problema P10.72, cuja solução era V2 = 4,33 m/s. (a) Use a teoria de escoamento gradualmente variado para estimar a profundidade da água 10 m a jusante na seção (3) para (a) declive de 5°, d
Considere o canal em forma de V da Figura PA10.7, com um ângulo arbitrário θ. Faça uma análise da continuidade e da quantidade de movimento para uma pequena perturbação δy que a velocidade de propagaç