Considere o canal em forma de V da Figura PA10.7, com um ângulo arbitrário θ. Faça uma análise da continuidade e da quantidade de movimento para uma pequena perturbação δy

que a velocidade de propagação da onda nesse canal é independente de θ, e não é igual ao resultado c0 = (gy)1/2 de canal largo.

Nessa questão, vamos usar uma abordagem igual àquela utilizada na seção “Velocidade da onda de superfície”, demonstrada na página 709.

Primeiro, nós temos que considerar uma perturbação de altura e velocidade , como demonstra a imagem abaixo:

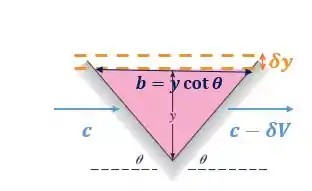
Note que a largura da superfície livre do canal é . Além disso, perceba que a velocidade de saída no nosso volume de controle é uma velocidade qualquer.

Em seguida, vamos utilizar a equação da continuidade pra fazer o seguinte balanço:

Reorganizando a equação, a gente chega à seguinte expressão pra :

Agora, vamos expressar a relação de quantidade de movimento como um balanço entre a força líquida de pressão hidrostática e o fluxo líquido de quantidade de movimento:

Note que o termo de no lado esquerdo do balanço de forças indica o centroide do triângulo, pois a força hidrostática está aplicada bem no centro da geometria.

Reorganizando toda essa equação e substituindo da equação da continuidade que a gente calculou lá em cima, a gente obtém:

Que é diferente do valor obtido na dedução feita pelo livro.